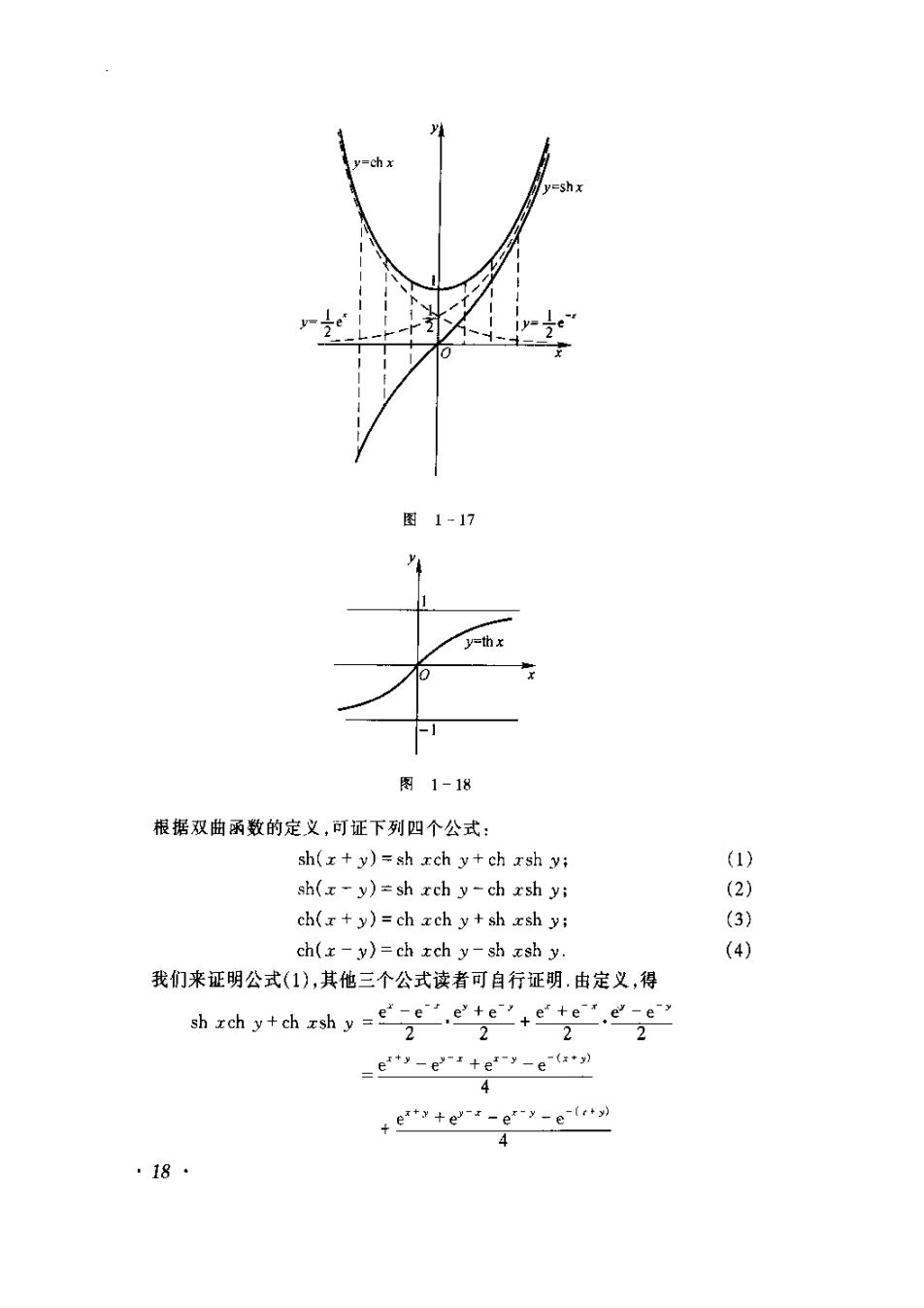
峰=ch xy=shx图1-17y=thx-1图1-18根据双曲函数的定义,可证下列凹个公式:(1)sh(r+y)=sh ach y+ch sh y;(2)sh(y)= sh rch y-ch rsh yi(3)ch(r +y)=ch ach y+sh ash y;(4)ch(r-y)=ch xch y-sh zsh y.我们来证明公式(1),其他三个公式读者可自行证明,由定义,得ee.e'te'+e'te.e-e"shchy+chshy=2222e**y-e'"++e*y-e'(+)4-(ity)x+y+e"-ey-A418

e*ty-e'(2n)=sh(r + y)2由以上几个公式可以导出其他一些公式,例如:在公式(4)中令=y并注意到ch0=1,得ch'-sh'r= l :(5)在公式(1)中令r=y.得(6)sh 2x=2sh xch ±;在公式(3)中令=,得(7)ch 2= ch'++sh'以上关于双曲函数的公式(1)至(7)与三角函数的有关公式相类似,把它们对比一下可帮助记忆双曲函数y=sh,y=ch(r≥0),y=th的反函数依次记为反双曲正弦y=arsh ,反双曲余弦y=arch,反双曲正切Jy=arthI.这些反双曲函数都可通过自然对数函数来表示,分别讨论如下:y=arsha是r=shy的反函数,因此,从r-e-e'2中解出y来便是arsh.令u=e,则由上式有u2-2xu-1=0.这是关于u的一个二次方程,它的根为u=r+i因u=e">0,故上式根号前应取正号,于是u=r+r+i由于y=Inu,故得y=arsh =ln(r+V?+1)函数y=arsh元的定义域为(-8o,+o),它是奇函数,在区间(0o,+o)内为单调增加,由y=shr的图形,根据反函数的作图法,可得y=arsh的图形如图1-19所示下面讨论双曲余弦y=ch(≥0)的反函数.由=chy(y≥0),有r=e'+e'y"y≥02由此得e=±-1故y=In(x+-1)·19

上式中元的值必须满足条件r1,而其中平方根前的符号由于y0应取正,故y-in(r+Vr?-i)上述双曲余弦y-chr(x≥0)的反函数称为反双曲余弦的主值,记作=arch,即y=archr=ln(r+yr-1)这样规定的函数y=arch的定义域为[1,+),它在区间[1,+co)上是单调增加的(图1-20)YHy-archxy=arsh x0图1-19图1-20类似地可得1+ y-arthx1这函数的定义域为开区间(-1,1),它在开区间(-1,1)内是单调增加的奇函数它的图形关于原点对称(图1-21)yarth x图1-21习题1-11.设A=(-8,-5)U(5,+),B=[-10,3),写出AUB,AnBAIB及AI(AIB)的表达式.2.设A、B、C是任意三个集合,证明对偶律:(AΛB)C=AUB3.设映射f:X→Y.ACX,BCX.证明(1) (AUB)-(A)Uf(B);·20

(2)f(ANB)C/(A)NF(B)4.设映射f:X+Y,若存在一个映射g:Y→X,使g°=,t°g=1,其中Ix、1、分别是X,Y上的恒等映射,即对于每一个rEX,有Ix=r;对于每一个yEY,有Iv=v.证明:f是双射,且g是f的逆映射:g=f!5.设映射:X→Y,ACX.记f(A)的原像为/((A))证明:(I) f-I(F(A))DA;(2)当f是单射时,有F((A))=A.6.求下列函数的自然定义域:1(1) y=V3.r +2;(2) y-1-1(3) y= /1-7;(4) y-V4-4(6) y= lan(1 +1);(5)y=sinVx;(8)y=/3-+aretan(7) y=urcsin(r-3);(10)y=et(9) y=ln(r+1);7.下列各题中,函数()和g()是否相同?为什么?(1) f(x)=lgx, g()=2ig r:(2) f(α)=r, g(α)-VT;(3)(r)=V-,8()=V-1;(4) f()=1, g(r)-secr tan'8.设sin al,Il<p(r)-Ial>f.0,求(()(),(-2),并作出函数()的图形9.试证下列函数在指定区间内的单调性:(-00,1);(1) y=r(2) y=r+ln t, (0, +o)10.设()为定义在(-1,1)内的奇函数,若/)在(0,1)内单调增加,证明()在(1,0)内也单调增加11.设下面所考虑的效都是定义在区间(一,1)上的证明:(1)两个偶函数的和是偶函数,两个奇函数的和是奇函数;(2)两个偶函数的乘积是偶函数,两个奇函数的乘积是偶函数,偶函数与奇函数的乘积是奇函数21

12,下列函数中哪些是偶函数,哪些是奇函数,哪些既非偶函数又非奇函数?(2) y-3r2 -r;(1) y=a(1-1):1-22(3) y -(4) y=.t(x -1)(x +1) :1+:(6) y=a ta*(5) y= sin -cos r +1:1213.下列各函数中哪些是周期函数?对于周期函数,指出其周期:(1) y= cos(a2);(2)y-Lo9 4;(3)y=1+sin 元x;(4) y=rcos z:(5) y= sin 14.求下列函数的反函数:1(1) y=r+l;(2)y1+(3) y=ar th(中《《中)(4)y=2sin 3(ad·bc#0);crtd2°(6) y=21(5) y=1+ ln(±+2);15.设函数f(.r)在数集X上有定义,试证:函数(x)在X上有界的充分必要条件是它在X上既有上界又有下界,16.在下列各题中,求由所给函数构成的复合函数,并求这函数分别对应于给定自变量值,和的函数值:2(1) y=.u=sins2=-n=号:元(2) y=sin n.u=2,2=-"号;(3) y=/u,u-1++*., =1.r2 =2;(4) y=e,u=r2,1, =0.32 -l;(5) y=u2,u=et,T, =1,r2=- 1.17.设()的定义域D=[0,1].求下列各函数的定义域:(1) /(.);(2) f(sin r):(4)(+a)+f(r)(a>0)(3) f(xa) (a>0);18.设1-/<1,1,(2)=30.1al=l, g(x)=e*,(-1, Iz[>1,求g()和g[),并作出这两个函数的图形19,已知水巢的横断面为等腰梯形,斜角9=40(图1-22).当过水断面ABCD的面积为定值S。时,求湿周L(IL=AB+BC+CD)与水深h之间的函数关系式,并指明其定义域20.收音机每台售价为90元,成本为60元.厂方为鼓励销售商大量采购,决定凡是订购量超过100台以上的,每多订购1台,售价就降低1分,但最低价为每台75元.22·