
第二节平面及其方程
第二节 平面及其方程

曲面方程与空眉间一曲线方程概念
一、曲面方程与空间 曲线方程概念
>曲面方程概念如果曲面s与方程F(x,y,z)=0有下述关系:F(x, y,z)= 0(1)曲面S上的任意点的坐标都满足此方程;(2)不在曲面S上的点的坐标不满足此方程S则F(xy,z)=0叫做曲面S的方程y曲面S叫做方程F(x,y,2)=0的图形>曲线方程概念空间曲线可视为两曲面S,S,的交线F(x,y,z)= 0Si方程组S2G(x, y,z)= 0F(x,y,)=0G(x,y,z) = 0称为空间曲线C的方程曲线C称为方程组的图形
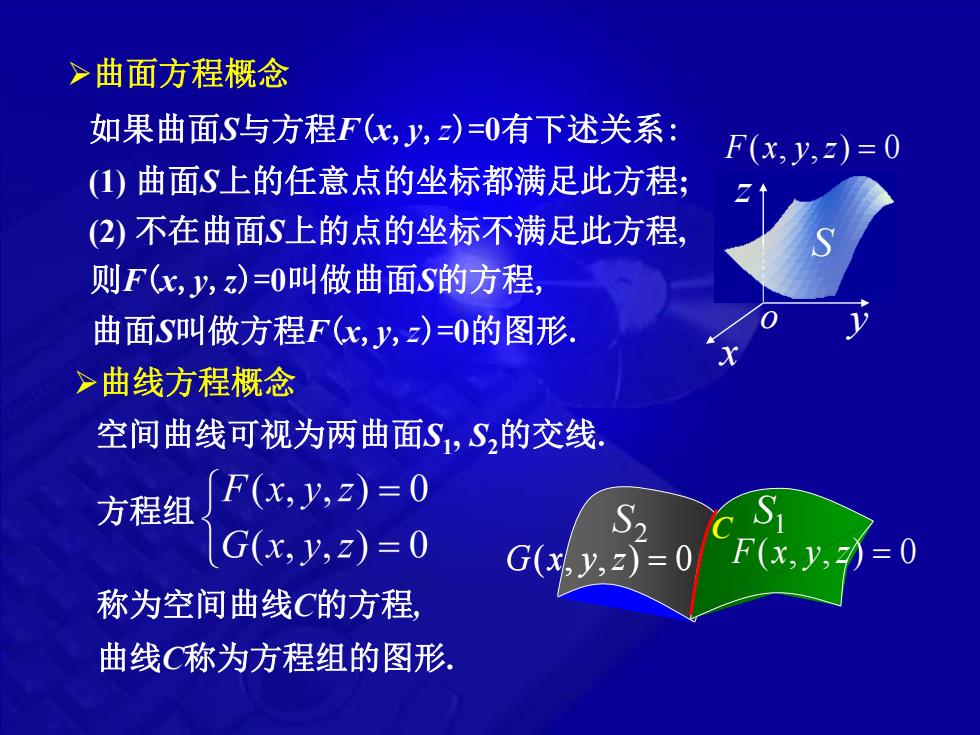
F(x, y,z) 0 S z y x o 如果曲面S与方程F(x,y,z)=0有下述关系: (1) 曲面S上的任意点的坐标都满足此方程; 则F(x,y,z)=0叫做曲面S的方程, 曲面S叫做方程F(x,y,z)=0的图形. (2) 不在曲面S上的点的坐标不满足此方程, 曲面方程概念 曲线方程概念 空间曲线可视为两曲面S1 , S2的交线. S2 G(x, y,z) 0 F(x, y,z) 0 S1 G(x, y,z) 0 方程组 C 称为空间曲线C的方程, 曲线C称为方程组的图形

平面的点法式方程二
二、平面的点法式方程

>方程的建立通过点 M。(xo,Yo,o)设平面ⅡI垂直于非零向量n=(A,BC),法向量任取 M(x,y,z)e II,YMoMInMoM.n=0MoM = (x-Xo,y-yo,z-zoA(x - xo)+ B(y- yo)+C(z - zo) = 0平面Ⅱ的点法式方程
z y x o M0 n ( , , ) 0 0 0 0 通过点 M x y z 垂直于非零向量 ( ) ( ) ( ) 0 A x x0 B y y0 C z z0 M 平面的点法式方程 设平面 M ( x, y,z) , n (A , B, C), M M n 0 0 M 0M n 任取 方程的建立 法向量