
函数的定义域通常按以下两种情形来确定:一种是对有实际背景的函数,根据实际背景中变量的实际意义确定.例如,在自由落体运动中,设物体下落的时间为t,下落的距离为,开始下落的时刻t=0,落地的时刻t=T,则s与t之间的函数关系是1S=gt', tE[0, T].这个函数的定义域就是区间[0,T];另一种是对抽象地用算式表达的函数,通常约定这种函数的定义域是使得算式有意义的一切实数组成的集合,这种定义域称为函数的自然定义域在这种约定之下,一般的用算式表达的函数可用“y=()表达,而不必再表出D,例如,函数=1-的定义域是闭区间1的定义域是开区间(-1,1)[-1,1],函数y=V1-r在函数的定义中,对每个ED,对应的函数值总是唯一的,这样定义的函数称为单值函数,如果给定一个对应法则,按这个法则,对每个ED,总有确定的值与之对应,但这个不总是唯一的,我们称这种法则确定了一个多值函数.例如,设变量和之间的对应法则由方程+=2给出,显然,对每个[-,],由方程+y=可确定出对应的y值,当=或-时,对应y=0一个值;当1取(一r,r)内任一个值时,对应的有两个值.所以这方程确定了二个多值函数.对于多值函数,往往只要附加一些条件,就可以将它化为单值函数,这样得到的单值函数称为多值函数的单值分支例如,在由方程+=给出的对应法则中,附加"≥0"的条件,即以?+y=且≥0"作为对应法则,就可得到一个单值分支=()=-,附加"≤0"的条件,即以"2+y二且≤0"作为对应法则,就可得到另一个单值分支=y(x)=--表示函数的主要方法有三种:表格法、图形法、解析法(公式法),这在中学里大家已经熟悉.其中,用图形法表示函数是基于函数图形的概念,即坐标平面上的点集(P(x+y)y=f(r),rED)称为函数y=f(),ED的图形(图1-3).图中的R,表示函数=f()的值城.下面举几个函数的例子例5函数=2的定义域D=(-,+8),值域W=121,它的图形是一条平行于x轴的直:8:
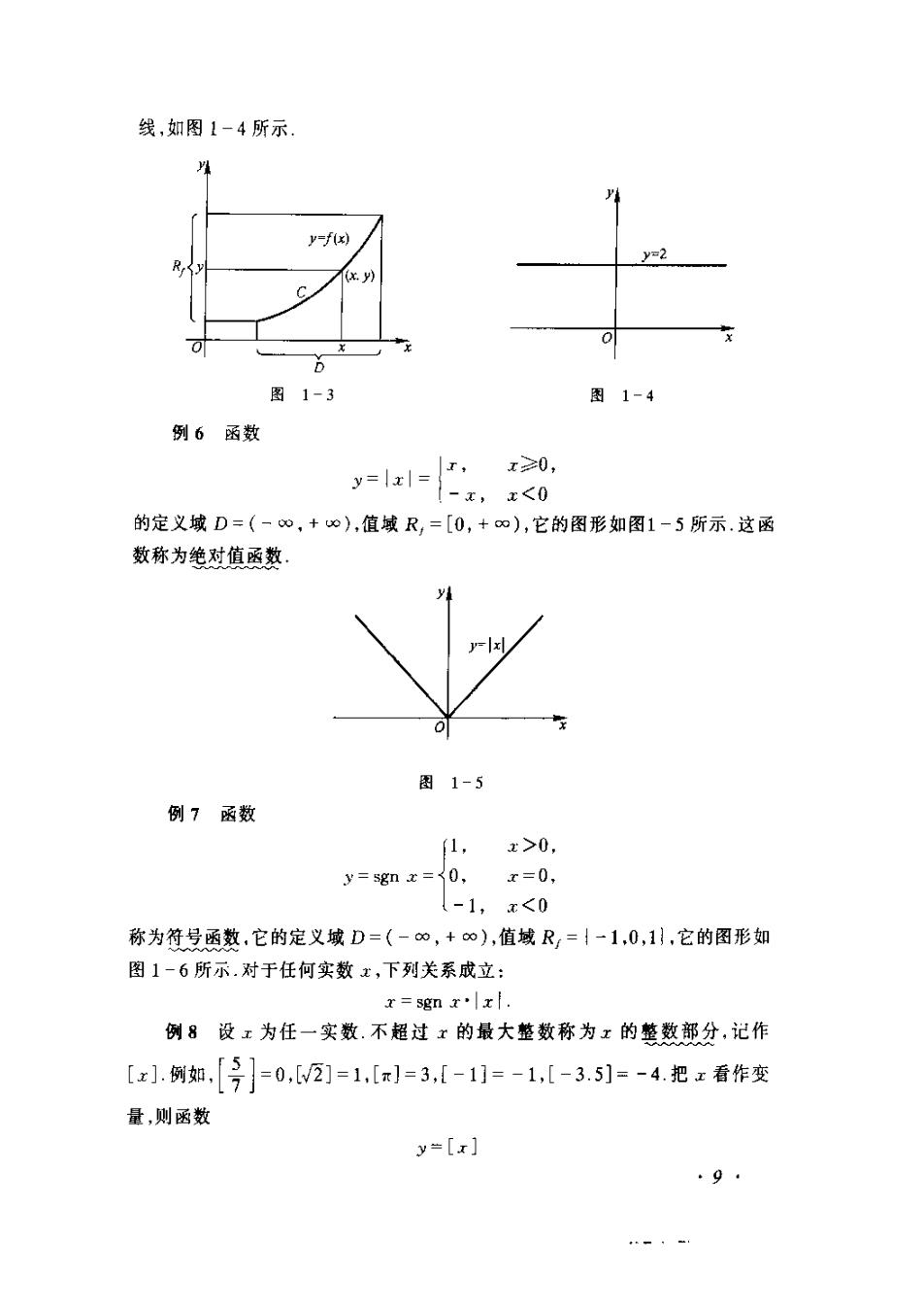
线,如图1-4所示,以yy=f(x)y=2R(x. y)$xooYD图1-3图1-4例6函数1≥0y=lrl2<0,的定义域D=(-,+),值域R,=[0,+8o),它的图形如图1一5所示.这函数称为绝对值函数,yIo图1-5例7函数z>0,[1,r=0,y=sgn =^0,(-1, x<0称为符号函数,它的定义域D=(-80,+α).值域R,=/-1,0,11,它的图形如图1-6所示.对于任何实数元,下列关系成立:r= sgn |xl.例8设工为任一实数.不超过的最大整数称为工的整数部分,记作[].例如=0,[V/2]=1,[元]=3,[-1]=-1,[-3.5]=-4.把r看作变量,则函数y=[α]9

yIy-[x]2yiy=sgn x234x-4 -3 -2 -11092o1x00-2图1-6图1-7的定义域D=(-00,+0),值域R,=Z.它的图形如图1-7所示,这图形称为阶梯曲线.在为整数值处,图形发生跳跃,跃度为1,这函数称为取整函数在例6和例7中看到,有时一个函数要用几个式子表示这种在自变量的不同变化范围中,对应法则用不同式子来表示的函数,通常称为分段函数例9函数[2V,0≤≤1,y=f(a)=(1+a, r>1是一个分段函数.它的定义域D=[0,+8).当ytrE[01]时,对应的函数值f()=2:当E(1,+00)时,对应的函数值f(r)=1+z.例/=12;16e[0,1],所以于(1)=2如,V22.[0,1],所以f(1)=2/1=2;3E(1,+00),所以f(3)=1+3=4.这函数的图形如图1-8所示用几个式子来表示一个(不是几个!函数,0不仅与函数定义并无矛盾,面且有现实意义.在自然科学和工程技术中,经常会遇到分段函数图 1-8的情形.例如在等温过程中,气体压强力与体积V的函数关系,当V不太小时依从玻意耳定律;当V相当小时,函数关系就要用范德瓦耳斯方程来表示,即.10

kV≥Vi,V力二YV<V.V-βV)其中k、α、β、Y都是常量2.函数的几种特性(1)函数的有界性设函数f(x)的定义域为D,数集XCD.如果存在数K.使得f(r)≤K对任一EX都成立,则称函数f(r)在X上有上界,而K,称为函数f()在X上的一个上界,如果存在数K,,使得f()≥K,对任一EX都成立,则称函数f()在X上有下界,而K,称为函数f()在X上的一个下界.如果存在正数M,使得[f(r)/≤M对任一rEX都成立,则称函数(r)在X上有界.如果这样的M不存在,就称函数f()在X上无界;这就是说,如果对于任何正数M,总存在,EX,使1(,)>M,那么函数(α)在X上无界例如,就函数f()=sin在(-o,+α)内来说,数1是它的个上界,数一1是它的一个下界(当然,大于1的任何数也是它的上界,小于一1的任何数也是它的下界).又Isin r/≤1对任一实数都成立,故函数()=sin在(α,+o)内是有界的.这里M=1当然也可取大于1的任何数作为M而使1f(r)i≤M成立).又如函数F(z)=一在开区间(0,1)内没有上界,但有下界,例如1就是它的1在开区间(0,1)内是无界的,因为不存在这样的正数一个下界.函数f()=≤M对于(0,1)内的一切都成立(接近于0时,不有在确定的正M.使!r数K,使<K,成立).但是()-二在区间(1,2)内是有界的,例如可取MT=1而使一≤1对于一切(1,2)都成立.容易证明,函数f()在X上有界的充分必要条件是它在X上既有上界又有下界,.11
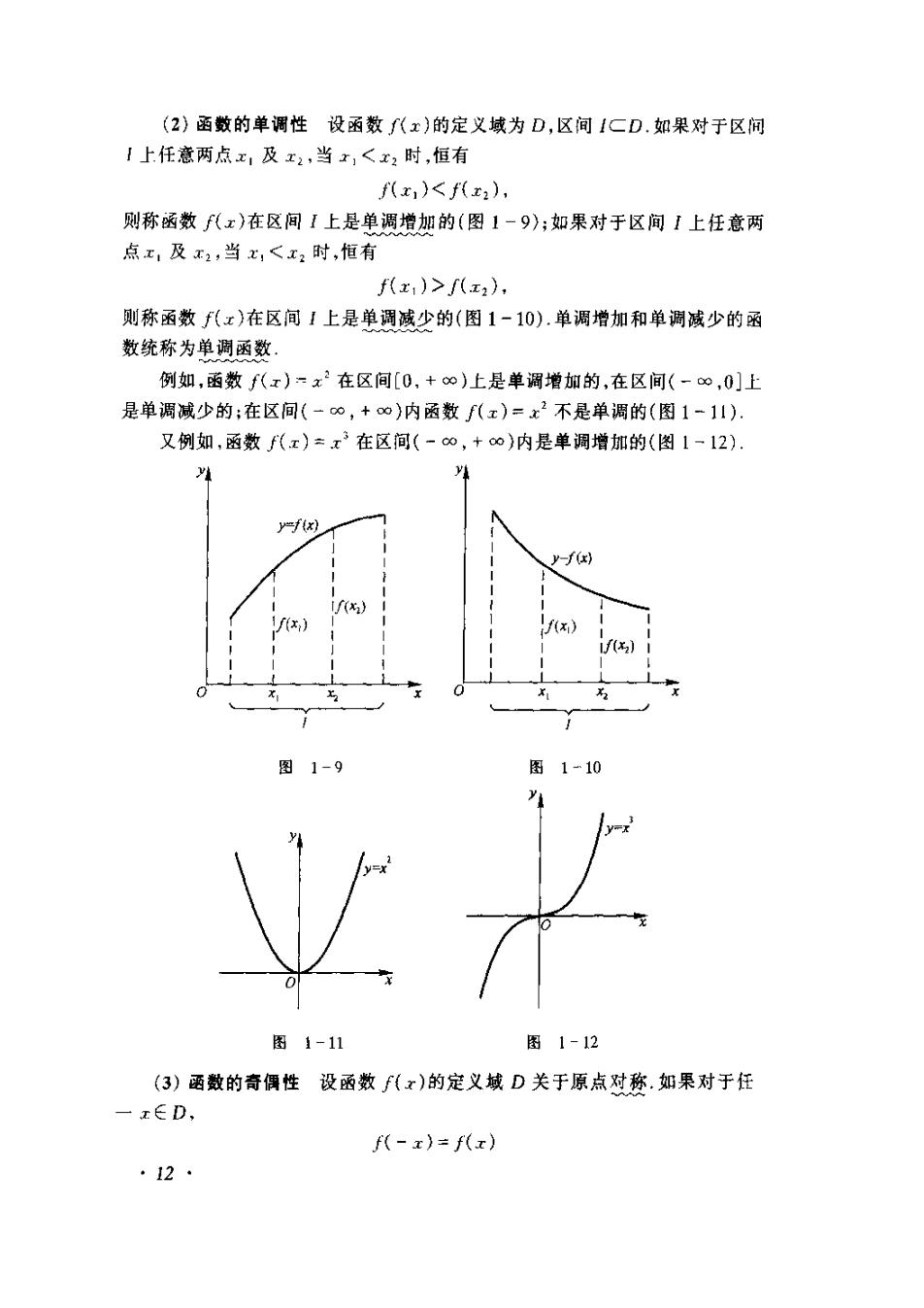
(2)函数的单调性设函数()的定义域为D,区间ICD.如果对于区间1上任意两点,及工,当,<时,恒有f(r)<f(r)则称函数f(z)在区间上是单调增加的(图1-9);如果对于区间I上任意两点元,及2,当,<,时,恒有f()>()则称函数f()在区间1上是单调减少的(图1-10).单调增加和单调减少的函数统称为单调函数,例如,函数f()在区间[0,+)上是单调增加的,在区间(-80,0]上是单调减少的;在区间(-0,+)内函数f()=不是单调的(图111)又例如,函数f()=在区间(-80,+0)内是单调增加的(图1-12)Yyy-f(x)y-f(x)i(x)1(x,)((x)if(r)OXI32x,X1图1-9图1-10y1图1-11图1-12(3)函数的奇偶性设函数F()的定义域D关于原点对称,如果对于任zED,f(-)=f().12