
第一节微分中值定理一、罗尔(Rolle)定理二、拉格朗日(Lagrange)中值定理三、柯西(Cauchy)中值定理
第一节 微分中值定理 一、罗尔( Rolle )定理 二、拉格朗日( Lagrange )中值定理 三、柯西( Cauchy )中值定理
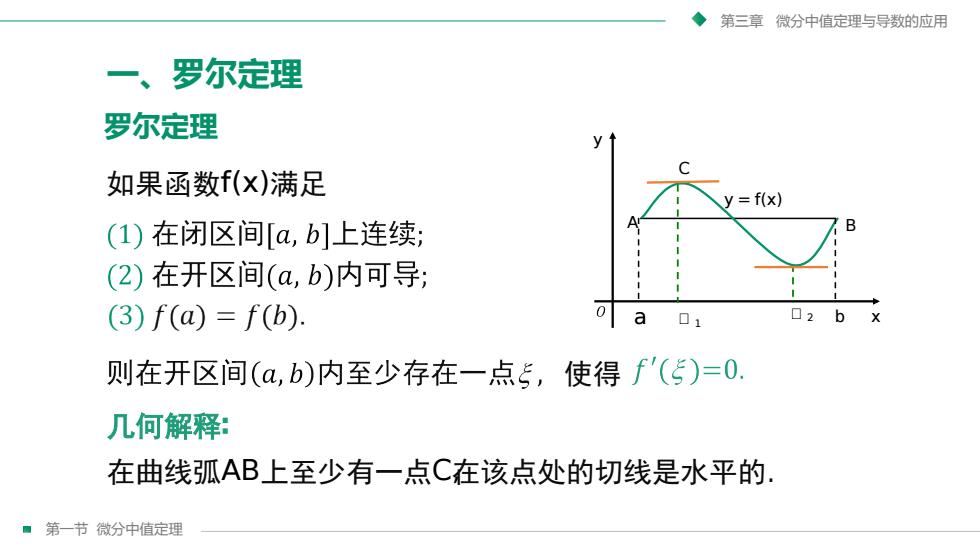
第三章微分中值定理与导数的应用一、罗尔定理罗尔定理C如果函数f(x)满足/= f(x)B(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;o□2b(3) f(a) = f(b).aX口1则在开区间(a,b)内至少存在一点,使得f'()=0几何解释:在曲线弧AB上至少有一点C在该点处的切线是水平的第一节微分中值定理
第一节 微分中值定理 第三章 微分中值定理与导数的应用 一、罗尔定理 x y y = f(x) ᵱ ᵱ 2 1 A B a b C 罗尔定理 如果函数f(x)满足 使得 几何解释∶ 在曲线弧AB上至少有一点C,在该点处的切线是水平的

第三章微分中值定理与导数的应用证:f(x)在[ab]连续,必有最大值M和最小值m.(1)若 M = m. 则 f(x) = M. V E (ab),都有 f( )= 0.(2)若Mm.f(a)=f(b),最值不可能同时在端点取得.设M→f(a),则在(ab)内至少存在一点使f()=M.f(≤+ △x) -f(5)+≥0,: f"(5) = limAx4x-0-f(≤+△x) -f(5):(费马)只有f(口)=0f(5) =lim0AxAx-0+:f(口)存在,f_(口)=f+(口)第一节微分中值定理
第一节 微分中值定理 第三章 微分中值定理与导数的应用 证 ∵ f(x) 在 [a,b] 连续, 必有最大值 M 和最小值 m. (1) 若 M = m. 则 f(x) = M. ∀ ᵱ ∈ (a,b),都有 f ′ (ᵱ ) = 0. (2) 若 M ≠ m. ∵ f(a) = f(b), ∴ 最值不可能同时在端点取得. 设 M ≠ f(a), 则在 (a,b) 内至少存在一点 ᵱ 使 f(ᵱ ) = M. ∵ f ′ (ᵱ )存在, ∴ f ′ −(ᵱ ) = f ′ +(ᵱ ). ∴ (费马)只有 f ′ (ᵱ ) = 0

第三章微分中值定理与导数的应用二、拉格朗日中值定理J拉格朗日定理y=f(x)-B如果函数f(x)满足D(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导xOa5152bf(b) -f(a)则在开区间(α,b)内至少存在一点气使得f()=b-a几何解释在曲线弧AB上至少有一点C在该点处的切线平行于弦AB.第一节微分中值定理
第一节 微分中值定理 第三章 微分中值定理与导数的应用 二、拉格朗日中值定理 拉格朗日定理 如果函数f(x)满足 使得 几何解释∶ 在曲线弧 AB 上至少有一点 C,在该点处的切线平行于弦AB

第三章微分中值定理与导数的应用证方法1.设辅助函数: Φ(x)f(b) -f(a)p(x) = f(x) -Xb-a在[ab]上连续在(ab)内可导则(x)满足罗尔定理条件β(a) = (b):3E(ab)使得@)=0.f(b) -f(a)=0bf(a)-af(b)即β'()= f() -b-ab-af(b) -f(a):f'() :证毕b-a第一节微分中值定理
第一节 微分中值定理 第三章 微分中值定理与导数的应用 证 方法1. 设辅助函数 则φ(x)满足罗尔定理条件, ∴ ∃ᵱ ∈ (a,b),使得 φ′ (ᵱ ) = 0. = 0. 证毕 ∵ φ(x) 在[a,b]上连续, 在(a,b)内可导, φ(a) = φ(b)