
第五节函数的极值与最大值最小值一、函数的极值及其求法最大值最小值问题二
第五节 函数的极值与最大值最小值 一、函数的极值及其求法 二、最大值最小值问题

第三章微分中值定理与导数的应用一、函数的极值及其求法1.函数极值的定义设函数f(x)在点xo的某邻域U(xo)内有定义如果对于去心邻域U(xo)内的任一x,有x0f(x)<f(xo)(或f(x) ≥> f(xo))Xo定义则称f(xo)是函数f(x)的一个极大值(或极小值)V函数的极大值与极小值统称为极值使函数取得极值的点Xo(自变量)称为极值点0Xo第五节承数的极值与最大值最小值
第五节 函数的极值与最大值最小值 第三章 微分中值定理与导数的应用 一、函数的极值及其求法 函数的极大值与极小值统称为 1. 函数极值的定义 定义 极值. 使函数取得极值的点x0(自变量)称为 f(x) < f(x0) 极值点

第三章微分中值定理与导数的应用注由图可知,在一个区间内(1)函数的极值只是一点附近的最大值或最小值是局部性的(2)函数可能存在许多个极值极小值可能大于某个极大值则f(×)=0(3)若f(x)在Xo点取得极值,或f(X。)不存在未取得极值口1尖点:一阶导不存在驻点:y=f(x)一阶导数等于零的点1-口口口口4日日4x,口第五节函数的极值与最大值最小值
第五节 函数的极值与最大值最小值 第三章 微分中值定理与导数的应用 驻点: 一阶导数等 于零的点 注 未取得极值 尖点:一阶导不存在 (2)函数可能存在许多个极值极小值可能大 , 于某个极大值. ᵯ1 ᵯ2 ᵯ3 ᵯ4 ᵯ5 ᵯ6 ᵯ ᵯ ᵯ ᵯ ᵯ (1)函数的极值只是一点附近的最大值或最小值,是局部性的. (3)若f(x)在x0点取得极值, 则f ′ (x0) = 0 或f ′ (x0)不存在
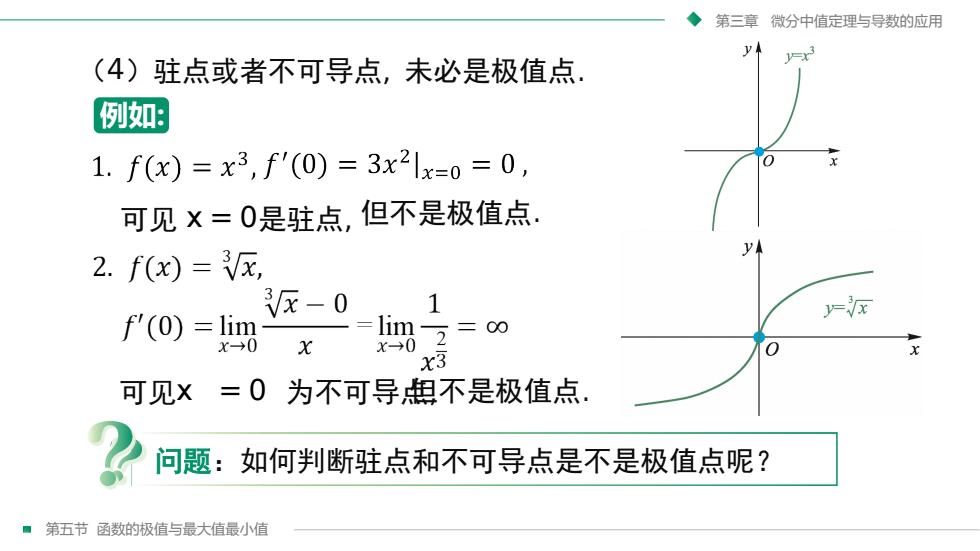
第三章微分中值定理与导数的应用V(4)驻点或者不可导点,未必是极值点例如:+1. f(x) = x3, f'(0) = 3x2|x=0 = 0,可见×=0是驻点,但不是极值点.y2. f(x) = x,3x-01J-xf(0) = limlim82x-→0xx-00xx3=0为不可导不是极值点.可见x问题:如何判断驻点和不可导点是不是极值点呢?第五节函数的极值与最大值最小值
第五节 函数的极值与最大值最小值 第三章 微分中值定理与导数的应用 例如: (4)驻点或者不可导点, 未必是极值点. 可见 x = 0是驻点, 但不是极值点. 可见x = 0 为不可导点但不是极值点 , . 问题:如何判断驻点和不可导点是不是极值点呢?

第三章微分中值定理与导数的应用2.函数极值的求法定理1(必要条件设函数f(x)在xo处可导,且在xo处取得极值,则f(xo)=0.几何上(如下图)若Xo是连续函数f(x)单增单减的分界点,则Xo必为极值点xoxoox0totoXo40驻点情形不可导点情形第五节函数的极值与最大值最小值
第五节 函数的极值与最大值最小值 第三章 微分中值定理与导数的应用 几何上(如下图), 2. 函数极值的求法 定理1 (必要条件 ) 若x0是连续函数f(x)单增单减的分界点, 则x0必为极值点