
第三节泰勒公式泰勒公式的建立二、几个初等函数的麦克劳林公式三、泰勒公式的应用
第三节 泰勒公式 一、泰勒公式的建立 二、几个初等函数的麦克劳林公式 三、泰勒公式的应用
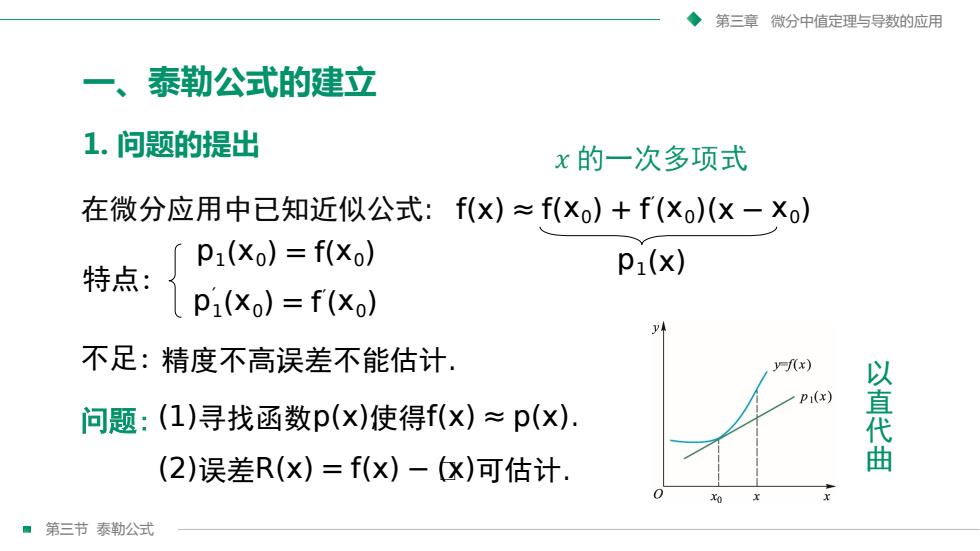
第三章微分中值定理与导数的应用泰勒公式的建立1.问题的提出x的一次多项式在微分应用中已知近似公式:f(x)~f(Xo)+f(X)(×一Xo)pi(Xo) = f(Xo)pi(x)特点:pi(xo) = f(xo)y4不足:精度不高误差不能估计,f(x)以直代曲pi(x)问题:(1)寻找函数p(x)使得f(x)~ p(x).(2)误差R(x) = f(x) 一(x)可估计.0+xXo第三节泰勒公式
第三节 泰勒公式 第三章 微分中值定理与导数的应用 一、泰勒公式的建立 1. 问题的提出 在微分应用中已知近似公式: f(x) ≈ f(x0) + f ′ (x0)(x − x0) p1(x) 特点: p1(x0) = f(x0) p ′ 1(x0) = f ′ (x0) 不足: 精度不高,误差不能估计. 问题: (1)寻找函数p(x),使得f(x) ≈ p(x). (2)误差R(x) = f(x) − ᵼ(x)可估计. 以 直 代 曲
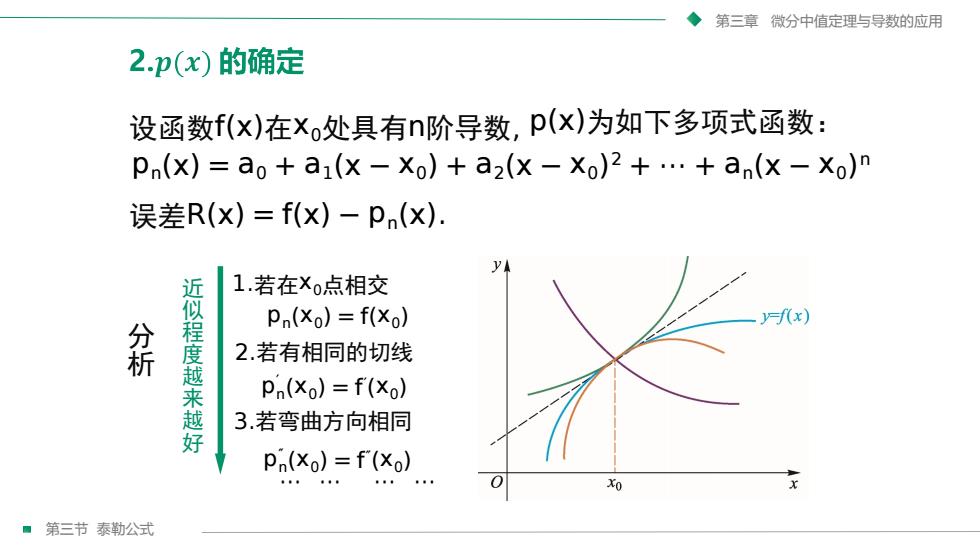
第三章微分中值定理与导数的应用2.p(x)的确定设函数f(x)在×。处具有n阶导数,p(x)为如下多项式函数:pn(x) = ao+ ai(x -xo) + a2(x-xo)2 + ... +an(x- Xo)r误差R(x) = f(x) - pn(x).yA1.若在×o点相交近似程度越来越好pn(×o) = f(×o)F(x)分析2.若有相同的切线pn(xo) =f(xo)3.若弯曲方向相同p,(xo) = f(xo)0XoX第三节泰勒公式
第三节 泰勒公式 第三章 微分中值定理与导数的应用 设函数f(x)在x0处具有n阶导数, p(x)为如下多项式函数: pn(x) = a0 + a1(x − x0) + a2(x − x0) 2 + ⋯ + an(x − x0) n 误差R(x) = f(x) − pn(x). 分 析 近 似 程 度 越 来 越 好 1.若在x0点相交 pn(x0) = f(x0) 2.若有相同的切线 p′ n(x0) = f ′ (x0) 3.若弯曲方向相同 p″ n(x0) = f ″ (x0) ⋯ ⋯ ⋯ ⋯

第三章微分中值定理与导数的应用求pn(x) = ao + ai(x- Xo) +a2(x -Xo)2 + ... + an(x -Xo)n要求pl (x0) = f(k)(x0)k = 0,1,2,...,n. 则1p(Xo) = f(xo)ao = f(xo)pn(xo) = f(Xo)1 ai = f(xo)1ak=kpr(xo) = f(xo)2! a2 = f(xo)(k = 0,1,2,...,n)p,(xo) = f"(xo)3! a3 = f(xo)p"(x0) = f(n)(x0) n!an = f(n)(xo)"(xo)xo)n:pn(x)=f(xo)+f'(xo)(x-xo)-2!n!第三节泰勒公式
第三节 泰勒公式 第三章 微分中值定理与导数的应用 求pn(x) = a0 + a1(x − x0) + a2(x − x0) 2 + ⋯ + an(x − x0) n 则 p(x0) = f(x0) a0 = f(x0) p′ n(x0) = f ′ (x0) 1 ⋅ a1 = f ′ (x0) p″ n(x0) = f ″ (x0) 2! ⋅ a2 = f ″ (x0) p‴ n(x0) = f ‴ (x0) 3! ⋅ a3 = f ‴ (x0) ⋯⋯⋯ ⋯

第三章微分中值定理与导数的应用3.泰勒中值定理泰勒中值定理1则存在的如果函数在处具有阶导数一个邻域,对于该邻域内的任一有f"(xo)f(x) = f(xo) + f'(xo)(x - xo)(x - xo)22!f(n)(xo)1(x-xo)n +o((x-xo)")+.n!其中幼=称为佩亚诺(余项1式称为函数在处的带有佩亚诺余项的阶泰勒公式,(或按(x一xo)的幂展开)第三节泰勒公式
第三节 泰勒公式 第三章 微分中值定理与导数的应用 3. 泰勒中值定理 泰勒中值定理1 如果函数ᵼ(ᵼ)在ᵼ0处具有ᵼ阶导数, 则存在ᵼᵼ的 一个邻域, 对于该邻域内的任一ᵼ,有 其中 ᵼᵼ(ᵼ) = ᵼ((ᵼ− ᵼ0) ᵼ)称为佩亚诺(ᵼᵼᵼᵼᵼ )余项. ① 式称为函数ᵼ(ᵼ)在ᵼ0处的带有佩亚诺余项的ᵼ阶泰勒公式. ①