
例5直线L绕另一条与L相交的直线旋转一周, 所得旋转曲面叫圆锥面两直线的交点叫圆锥 面的顶点,两直线的夹角a0<a<)叫圆锥 面的半顶角.试建立顶点在坐标原点,旋转轴 为z轴,半顶角为a的圆锥面方程 解y0z面上直线方程为 3 ycota M1(0,y1,1) 圆锥面方程 z=±x2+y2c0t M(x,y,2)
解 yoz面上直线方程为 z y cot 圆锥面方程 cot 2 2 z x y 5 . (0 ) 2 . . L L z 例 直线 绕另一条与 相交的直线旋转一周, 所得旋转曲面叫 两直线的交点叫圆锥 面的 ,两直线的夹角 叫圆锥 面的 试建立顶点在坐标原点,旋转轴 为 轴,半顶角为 的 圆锥面 顶点 半顶角 圆锥面方程 M( x, y,z) (0, , ) 1 1 1 M y z y x z O

圆锥面方程z=±√x2+y2cot z2=a2(x2+y2)(a=cota) a=1时,c0ta=1→a= 4 即圆锥面方程z2=x2+y2 (用得较多) 》0z面上直线方程为y=zcot@ 绕轴旋转所得曲面方程及图形 y=±Vx2+z2cota 即y2=cot2a(x2+z2) =a-(x2+2)(a=cota)
圆锥面方程 cot 2 2 z x y 即 圆锥面方程 ( ) ( cot ) 2 2 2 2 即 z a x y a a 1时, cot 1 4 2 2 2 z x y (用得较多) y z cot 绕y轴旋转所得曲面方程及图形. cot ( ) 2 2 2 2 y x z ( ) 2 2 2 a x z (a cot) y cot 即 yOz 面上直线方程为 2 2 x z O z x y
例6将下列各曲线绕对应的轴旋转一周,求 生成的旋转曲面的方程. x2 (1)双曲线 21 e=1分别绕x轴和轴 绕x轴旋转 =1 旋转双叶双曲面 绕z轴旋转 x2+y2 22 旋转单叶双曲面
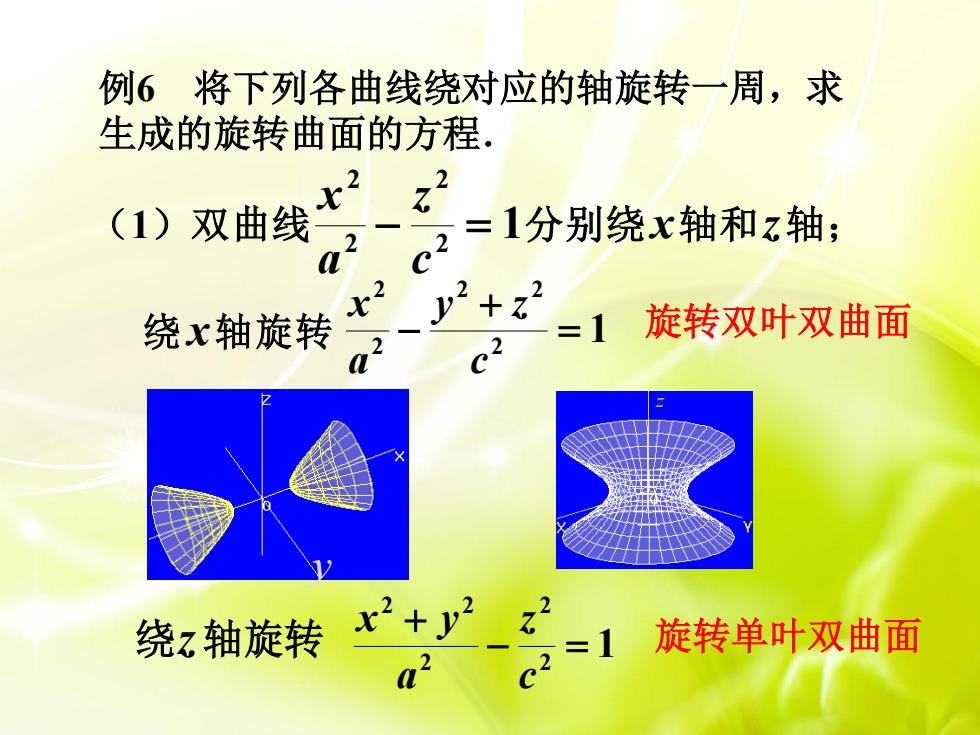
例6 将下列各曲线绕对应的轴旋转一周,求 生成的旋转曲面的方程. (1)双曲线 1 2 2 2 2 c z a x 分别绕 x轴 和z轴 ; 绕 x轴旋转 绕z轴旋转 1 2 2 2 2 2 c y z a x 1 2 2 2 2 2 c z a x y z 旋转双叶双曲面 旋转单叶双曲面 y

(2)椭圆 绕y轴和z轴; x=0 绕y轴旋转 之2 =1 绕z轴旋转 x2+y2 、22 =1 旋转椭球面 (3)抛物线 y2=2p2绕z轴: (x=0 x2+y2=2pz 旋转抛物面
(2)椭圆 0 1 2 2 2 2 x c z a y 绕 y轴和z轴; 绕 y轴旋转 绕z轴旋转 1 2 2 2 2 2 c x z a y 1 2 2 2 2 2 c z a x y 旋 转 椭 球 面 (3)抛物线 0 2 2 x y pz绕z轴; x y 2 pz 2 2 旋转抛物面