
第八章 第二节 数量积向量积*混合积 一、两向量的数量积 二、两向量的向量积 *三、向量的混合积
*三、向量的混合积 第二节 一、两向量的数量积 二、两向量的向量积 数量积 向量积 *混合积 第八章

两向量的数量积 引例.设一物体在常力F作用下,沿与力夹角为0 的直线移动,位移为了,则力F所做的功为 W=F‖3cos0 1.定义 M2 设向量a,b的夹角为0,称 记作 abcose ab W=F,5 为a与b的数量积(点乘积)
M1 一、两向量的数量积 沿与力夹角为 的直线移动, W = 1. 定义 设向量 的夹角为 ,称 记作 数量积 (点乘积) . 引例. 设一物体在常力 F 作用下, 位移为 s , 则力F 所做的功为 F s cos W F s = M2 a b 为a与b的 a, b s
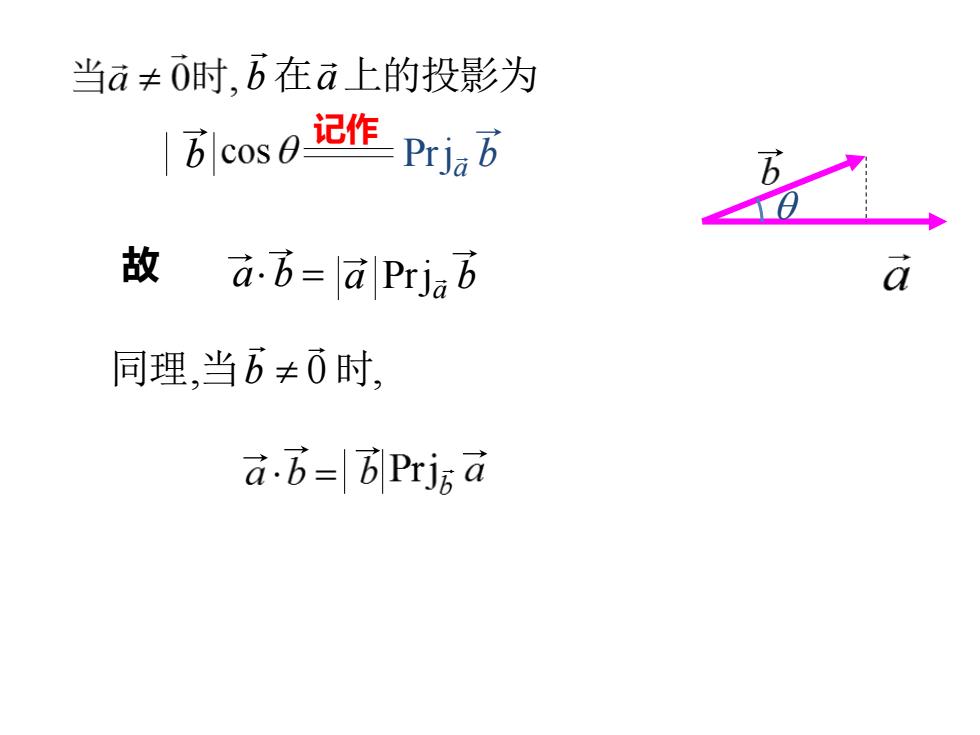
当a≠0时,b在a上的投影为 |6cos0记作prj,万 故 ab=a Priab 同理,当b≠0时, a.b=BPrjr a
b 在a上的投影为 记作 故 同理,当 0 时, b b Prja b a b = a Prja b

2.性质 (1)a.a-ap (2)a,为两个非零向量,则有 ab=0=a⊥b
2. 性质 为两个非零向量, 则有 (1) a a = (2) a,b a b = 0 ⊥

3.运算律 (1) 交换律a.b=b.d (2)结合律(2,u为实数) (b=a(b)=(a.b) (a).(ub)=a(a.(ub))=au(a.b) (3)分配律(a+b)c=d·c+bc
3. 运算律 (1) 交换律 (2) 结合律 a ( b) ( a)( b) = ( a ( b)) = (a b) (3) 分配律