
定义1设D是xOy平面上的点集,若变量z与D中的变量x,V之间有一个依赖关系,使得在D内每取定一个点P(x,y)时,按着这个关系有确定的z值与之对应,则称z是x,V的二元(点)函数.记为z= f(x,y)(或z = f(P))称x,y为自变量,称z为因变量,点集D称为该函数(zz = f(x, y),(x,y)eD,数集的定义域,称为该函数的值域
按着这个关系有确定的 点集D称为该函数 z = f (x, y) (或z = f (P)) 称为该函数的 zz = f (x, y),(x, y) D 则称z是x, y的 定义1 若变量z与D 中的变量x, y之间有一个依赖关系, 设D是xOy平面上的点集, 使得在D内 每取定一个点P(x, y)时, z值与之对应, 记为 称x, y为 的 数集 二元(点)函数. 自变量,称z为因变量, 定义域, 值域

函数z=f(x,J)在点 P(xo,yo)处的函数值记为 f(xo,yo)或f(P).类似,可定义n元函数二元及二元以上的函数统称为多元函数(2)多元函数定义域定义域为符合实际意义的实际问题中的函数:自变量取值的全体纯数学问题的函数:定义域为使运算有意义的自变量取值的全体
二元及二元以上的函数统称为 (2) 多元函数定义域 定义域为符合实际意义的 自变量取值的全体. 记为 函数 z = f (x, y) 在点 P(x0 , y0 ) 处的函数值 ( , ) 0 0 f x y ( ). P0 或 f 类似, 可定义n元函数. 多元函数. 实际问题中的函数: 自变量取值的全体. 纯数学问题的函数: 定义域为使运算有意义的
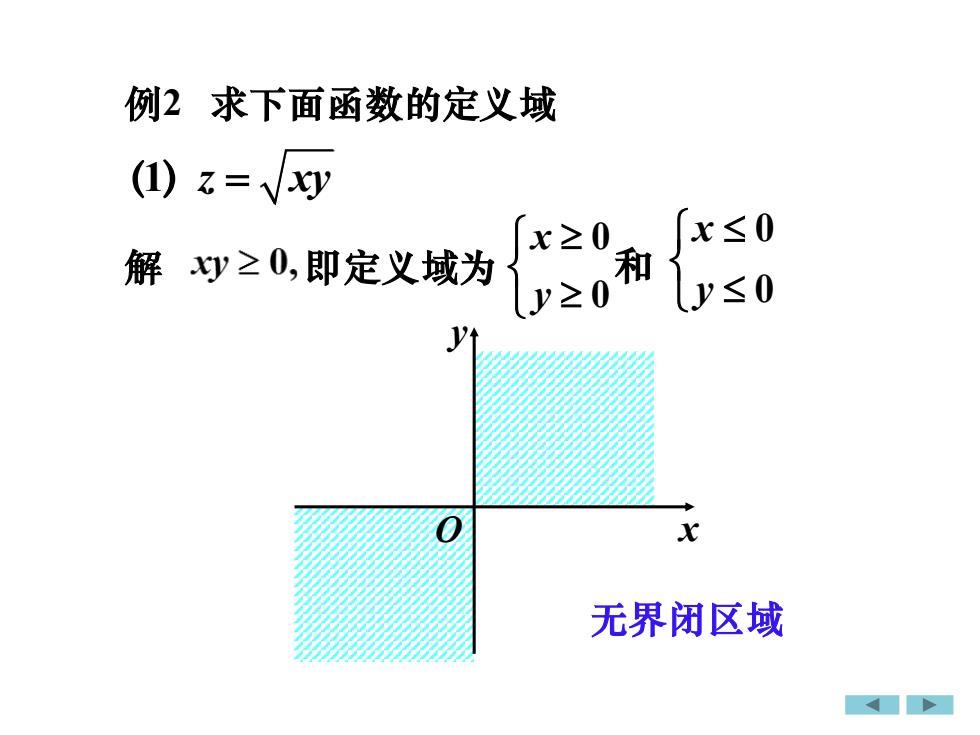
例2求下面函数的定义域(1) z= /xyx≤0x≥0和解y≥0,即定义域为y≤oy≥0Vx无界闭区域
例2 求下面函数的定义域 解 O x y 无界闭区域 (1)z xy = 0 0 x y 和 0 0 y x 即定义域为

/2x-x2 - y2(2) z= 1Vx?+y2-1解 定义域是(x-1)2+2≤1 且x2+2>1y0x有界半开半闭区域
• 1 解 O x y 2 2 2 2 2 2 1 x x y z x y − − = + − ( ) ( 1) 1 2 2 定义域是 x − + y 2 2 且x y + 1 有界半开半闭区域

用联立不等式表示下列平面闭区域Dy101直线圆弧D解域D有下列三种表示法:x?+y?≤1-1≤y≤0y≤02(1)1-y?≤x≤y+1x-y≤1-1≤x≤00≤x≤1及(3)1- x2x-1≤y≤0≤V≤0
用联立不等式表示下列平面闭区域 D . 圆弧 直线 解 域D有下列三种表示法: −1 x 0 0 x 1 x O y 1 − 1 − 1 (2) −1 y 0 1 1 2 − − y x y + (3) 1 0 2 − − x y 及 x −1 y 0 D 1 2 2 x + y y 0 x − y 1 (1)