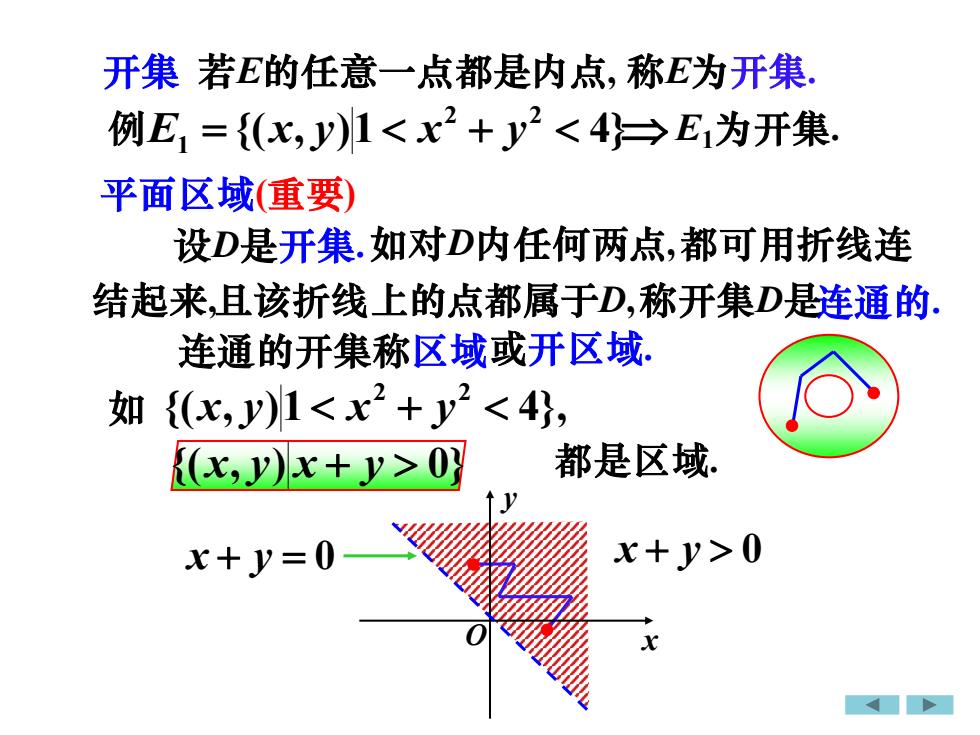
开集 若E的任意一点都是内点,称E为开集例E, =(x,)1<x2 +2<4)>Ei为开集平面区域(重要)设D是开集.如对D内任何两点,都可用折线连结起来,且该折线上的点都属于D,称开集D是连通的连通的开集称区域或开区域如 (x,y)1<x+ y<4)都是区域(x,y)x+ y>0)Jx+y>0x+y=0x
平面区域(重要) 设D是开集. 连通的开集称区域 连通的. 如对D内任何两点,都可用折线连 且该折线上的点都属于D,称开集D是 • 或开区域. 如 都是区域. {( , )1 4}, 2 2 x y x + y {(x, y) x + y 0} 开集 若E的任意一点都是内点, 例 {( , )1 4} 2 2 E1 = x y x + y 称E为开集. E1为开集. x + y = 0 x + y 0 O x y 结起来, • • •

开区域连同其边界,称为闭区域如((x,y)1≤x2 + y2≤ 4),(x, y)x+ y≥ 0)都是闭区域有界区域总可以被包围在一个以原点为中心、半径适当大的圆内的区域,称此区域为有界区域否则称为无界区域 (可伸展到无限远处的区域)
开区域连同其边界,称为 有界区域 否则称为 都是闭区域 . {( , )1 4}, 2 2 如 x y x + y {(x, y) x + y 0} 总可以被包围在一个以原点为中心、 适当大的圆内的区域, 称此区域为 半径 (可伸展到无限远处的区域 ). 闭区域. 有界区域. 无界区域
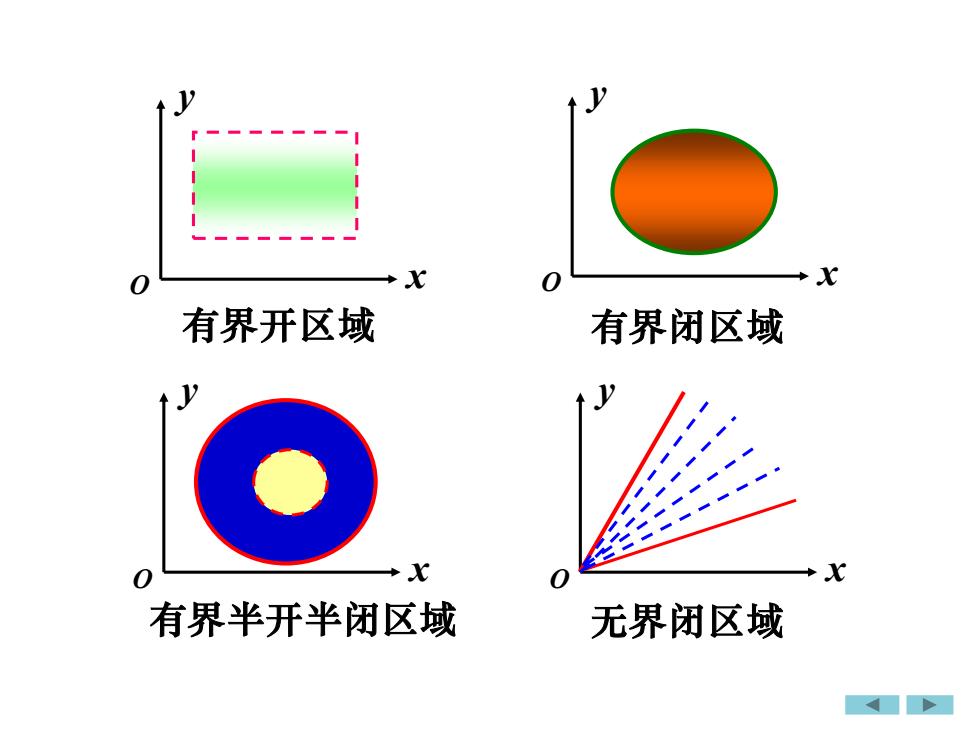
xx0有界开区域有界闭区域Lxx00有界半开半闭区域无界闭区域
O x y O x y O x y O x y 有界开区域 有界半开半闭区域 有界闭区域 无界闭区域

n元有序数组(xi,x2,,x,)的全体(2)n维空间称为n维空间.记作R";即R" = RxRx...xR=((x,x,..,x,)x, ER,i=1,2,..}.n 维空间中的每一个元素(xi,x2,,称为空间中的一个点,数x,称为该点的第k个坐标.n维空间中两点P(xi,X2,",xn)及Q(y1,J2,""",yn)的距离定义为PQ= /(x, - y)? +(x2 - y2)? +...+(x, - yn)n维空间中点P的8邻域为U(P,,)={PPP<3, PE R"}
n 元有序数组 的全体 ; n R n 维空间中的每一个元素 称为空间中 称为该点的第k个坐标. n维空间中两点 ( , , , ) 1 2 n P x x x 的距离定义为 2 2 2 2 2 1 1 ( ) ( ) ( ) n n PQ = x − y + x − y ++ x − y n 维空间中点 P0 记作 及 ( , , , ) 1 2 n Q y y y ( , ) { , }. 0 0 n U P δ = P PP δ P R 的邻域为 (2) n 维空间 称为n维空间. 即 {( , , ) , 1,2, }. x1 x2 xn xi R i = 的一个点, R = R R R = n

二、多元函数的概念1.二元函数的定义(1) 定义例1 理想气体的状态方程是pV=RT(R为常数)其中p为压强,V为体积,T为温度如温度T、体积V都在变化,则压强p依赖是P=RT于T,V的关系是L称p为两个变量T,V的函数,其中 0<T<+8,0 <V <+80
二、多元函数的概念 1. 二元函数的定义 例1 理想气体的状态方程是 V T p = R 称 p为两个变量T,V 的函数, 其中 (1) 定义 如温度T、体积V都在变化,则压强 p依赖 pV = RT (R为常数) 其中p为压强, V为体积, T为温度. 于T,V 的关系是 0 T + , 0 V +