
第七节方向导数与梯度1方向导数概念与计算公式1梯度概念与计算■数量场与向量场的概念■小结思考题
◼ 方向导数概念与计算公式 ◼ 梯度概念与计算 ◼ 小结 思考题 第七节 方向导数与梯度 ◼ 数量场与向量场的概念
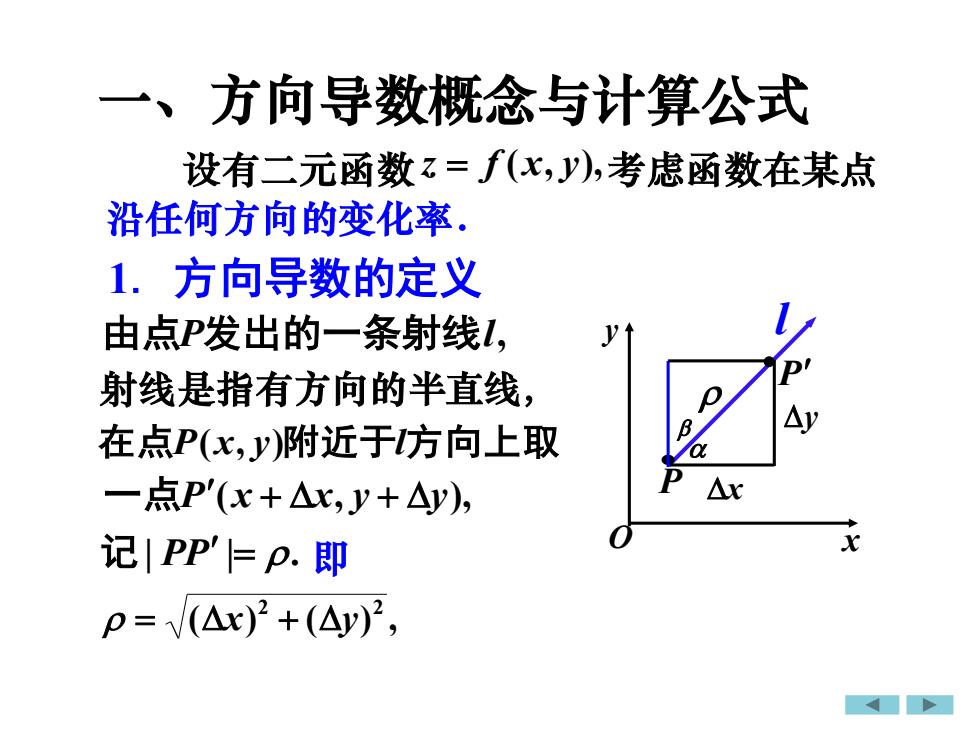
一、方向导数概念与计算公式设有二元函数z=f(x,J),考虑函数在某点沿任何方向的变化率。1.方向导数的定义由点P发出的一条射线l,P射线是指有方向的半直线AyB在点P(x.y)附近于访向上取DAx一点P'(x +Ax,y+Ay)Ox记|PP'=p.即p = /(△x)2 +(Ay)
1. 方向导数的定义 设有二元函数 z = f (x, y), 沿任何方向的变化率. 考虑函数在某点 射线是指有方向的半直线, 由点P发出的一条射线l, 在 点P(x, y)附近于l方向上取 一点P(x + x, y + y), 记| PP |= . 即 ( ) ( ) , 2 2 = x + y 一、方向导数概念与计算公式 x y • l • P x y O P

1f(P')- f(P)V定义如果极限limPP→PpOAyf(x+Ax,y+Ay)- f(x,y)B= limap-→0p Ar存在,则将这个极限值称为函数0x在点P沿方向的方向导数af即记为-aqaf(x+ △x, y + y) - f(x,y)limp-0p注方向导数是函数沿半直线方向的变化率
定义 如果极限 ( ) ( ) lim f P f P P P − → ( , ) ( , ) lim 0 f x + x y + y − f x y = → 存在,则将这个极限值称为函数 在点 P沿方向l的方向导数, 记为 , l f 即 ( , ) ( , ) lim 0 f x x y y f x y l f + + − = → 注 方向导数是函数沿半直线方向的变化率. x y P • l • P x y O
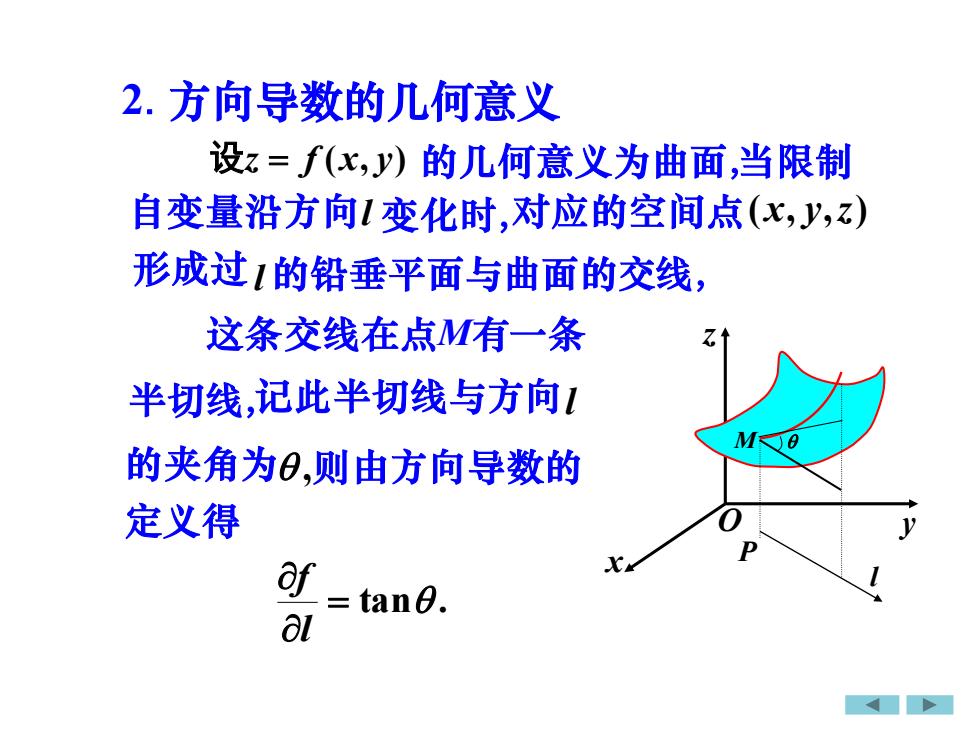
2.方向导数的几何意义设z=f(x,J)的几何意义为曲面,当限制自变量沿方向l变化时,对应的空间点(x,y,z)形成过1的铅垂平面与曲面的交线这条交线在点M有一条Z半切线,记此半切线与方向[MK6的夹角为,则由方向导数的0定义得yPaf1: tan0.al
x y z O 2.方向导数的几何意义 设z = f (x, y) 的几何意义为曲面,当限制 自变量沿方向 l 变化时,对应的空间点 (x, y,z) 形成过 l 的铅垂平面与曲面的交线, 这条交线在点M有一条 记此半切线与方向 l 的夹角为 , 则由方向导数的 = tan . l f 半切线, 定义得 M l P

注aff(x +△x, y+Ay)- f(x,y)= lim方向导数alp-→0O.p一定为正!是函数在某点沿任何方向的变化率aff(x+Ax,y)- f(x, y)lim偏导数axAxAr-→0aff(x, y+Ay)- f(x,y)limayAyAy-→0分别是函数在某点沿平行于坐标轴的直线的变化率,4x、4y可正可负!
( , ) ( , ) lim 0 f x x y y f x y l f + + − = → ρ一定为正! x f x x y f x y x f x + − = → ( , ) ( , ) lim 0 是函数在某点沿任何方向的变化率. 方向导数 偏导数 y f x y y f x y y f y + − = → ( , ) ( , ) lim 0 分别是函数在某点沿平行于坐标轴的直线 的变化率. Δx、Δy可正可负! 注