
全程设计 第五章 三角数 5.2 三角函数的概念 5.2.1 三角函数的概念 第1课时 三角函数的定义
第五章 三角函数 5.2 三角函数的概念 5.2.1 三角函数的概念 第1课时 三角函数的定义

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
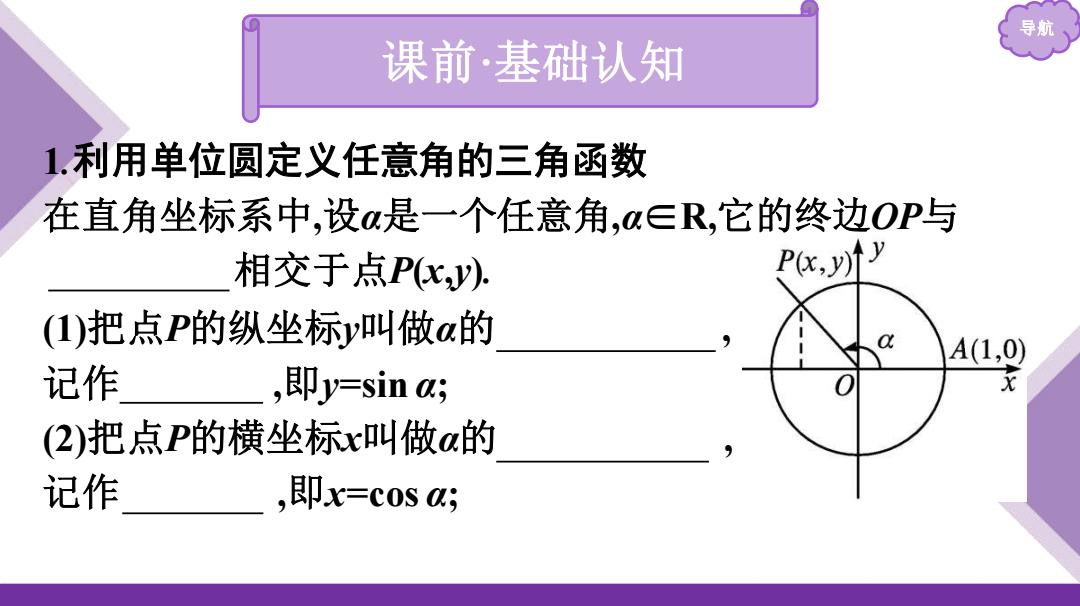
导航 课前·基础认知 1.利用单位圆定义任意角的三角函数 在直角坐标系中,设a是一个任意角,a∈R,它的终边OP与 相交于点Pcy), P化,yy (1)把点P的纵坐标叫做a的 A(1,0) 记作 ,即y=sina; (2)把点P的横坐标x叫做a的 记作 ,即x=Cosa;
导航 课前·基础认知 1.利用单位圆定义任意角的三角函数 在直角坐标系中,设α是一个任意角,α∈R,它的终边OP与 单位圆 相交于点P(x,y). (1)把点P的纵坐标y叫做α的 正弦函数 , 记作 sin α ,即y=sin α; (2)把点P的横坐标x叫做α的 余弦函数 , 记作 cos α ,即x=cos α;

导航 3)把点P的纵坐标与横坐标的比值兰叫做α的 ,记作 ,即=tana≠0).当≠0时,它也是以角为自变量,以 单位圆上的点的纵坐标与横坐标的比值为函数值的函数,称 为 我们将正弦函数、余弦函数和正切函数统称为
导航 (3)把点P的纵坐标与横坐标的比值 叫做α的 正切 ,记作 tan α ,即 =tan α(x≠0).当x≠0时,它也是以角为自变量,以 单位圆上的点的纵坐标与横坐标的比值为函数值的函数,称 为 正切函数 . 我们将正弦函数、余弦函数和正切函数统称为 三角函数 . 𝒚 𝒙 𝒚 𝒙

导 微总结(1)在任意角的三角函数的定义中,应该明确:x是一个 任意角,其范围是使函数有意义的实数集 (2)要明确sinx是一个整体,不是sin与x的乘积,它是正弦函数 的记号.离开自变量x的“sin“c0s“tan”都是没有意义的. (3)三角函数值是比值,是一个实数,这个实数的大小和点P化y) 在终边上的位置无关,与角的终边位置有关,对于确定的角, 其终边的位置也随之确定
导航 微总结(1)在任意角的三角函数的定义中,应该明确:x是一个 任意角,其范围是使函数有意义的实数集. (2)要明确sin x是一个整体,不是sin与x的乘积,它是正弦函数 的记号.离开自变量x的“sin”“cos”“tan”都是没有意义的. (3)三角函数值是比值,是一个实数,这个实数的大小和点P(x,y) 在终边上的位置无关,与角α的终边位置有关,对于确定的角α, 其终边的位置也随之确定