
全程设计 第五章 三角函数 5.4 三角国数的图象与性质 5.4.1 正弦函数、余弦函数的图象
第五章 三角函数 5.4 三角函数的图象与性质 5.4.1 正弦函数、余弦函数的图象

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
导航 课前·基础认知 正弦函数、余弦函数的图象 函数y=sinx V-cOS x y 3π -2π -2π 一兀 0 2π 3π 0 2π 3 2 3 图象 -1 -1 正弦函数y=sinx,x∈R的 余弦函数y=cosx,x∈R的图象叫做 图象叫做 ,是 ,它是与正弦曲线具有 一条“波浪起伏”的 相同形状的“波浪起伏”的 曲线 曲线
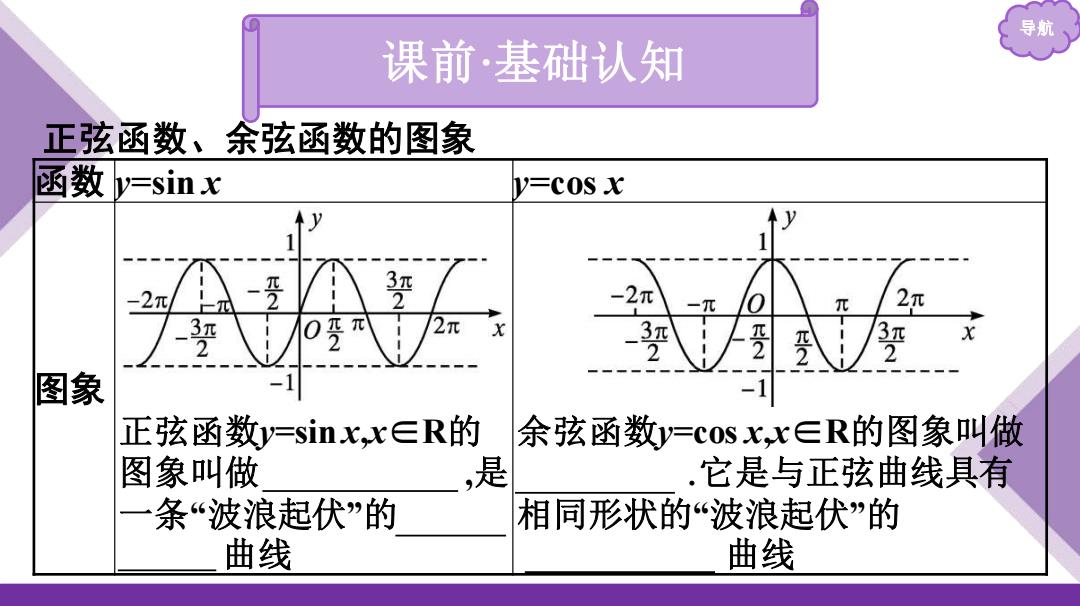
导航 课前·基础认知 正弦函数、余弦函数的图象 函数 y=sin x y=cos x 图象 正弦函数y=sin x,x∈R的 图象叫做 正弦曲线 ,是 一条“波浪起伏”的 连续 光滑 曲线 余弦函数y=cos x,x∈R的图象叫做 余弦曲线 .它是与正弦曲线具有 相同形状的“波浪起伏”的 连续光滑 曲线

导航、 函数 y=sin x v-cos x 图象 画法 “五点法” “五点法” 关键 (0,0), ,(元,0), (0,10, ,(π,-1), 五点 ,(2π,0) ,(2m,1)
导航 函数 y=sin x y=cos x 图象 画法 “五点法” “五点法” 关键 五点 (0,0), 𝛑 𝟐 ,𝟏 ,(π,0), 𝟑𝛑 𝟐 ,-𝟏 ,(2π,0) (0,1), 𝛑 𝟐 ,𝟎 ,(π,-1), 𝟑𝛑 𝟐 ,𝟎 ,(2π,1)

导航 微点拨五点法画图的优越性 ()避免了“描,点法”画图的烦琐,抓住了“描点法”的本质,使列 表更具有目标性,针对性。 (2)计算方便,描点准确. (3)由于抓住了关键点,所以更能准确反映图象全貌
导航 微点拨五点法画图的优越性 (1)避免了“描点法”画图的烦琐,抓住了“描点法”的本质,使列 表更具有目标性,针对性. (2)计算方便,描点准确. (3)由于抓住了关键点,所以更能准确反映图象全貌