
全程设计 第五章 三角函数 5.5三角恒等变换 5.5.2 简单的三角恒等变换
第五章 三角函数 5.5 三角恒等变换 5.5.2 简单的三角恒等变换

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 半角公式 sin 9
导航 课前 ·基础认知 半角公式 sin 𝜶𝟐 = ± 𝟏-𝐜 𝐨𝐬𝜶 𝟐 , cos 𝜶𝟐 = ± 𝟏 + 𝐜 𝐨𝐬𝜶 𝟐 , tan 𝜶𝟐 = ± 𝟏-𝐜 𝐨𝐬𝜶 𝟏 + 𝐜 𝐨𝐬𝜶

导航 因为不同的三角函数式不仅会有结构形式方面的差异,而且 还会存在所包含的角,以及这些角的三角函数种类方面的差 异,所以进行三角恒等变换时,常常要先寻找式子所包含的各 个角之间的联系,并以此为依据选择适当的公式,这是 的一个重要特点
导航 因为不同的三角函数式不仅会有结构形式方面的差异,而且 还会存在所包含的角,以及这些角的三角函数种类方面的差 异,所以进行三角恒等变换时,常常要先寻找式子所包含的各 个角之间的联系,并以此为依据选择适当的公式,这是 三角恒等变换 的一个重要特点
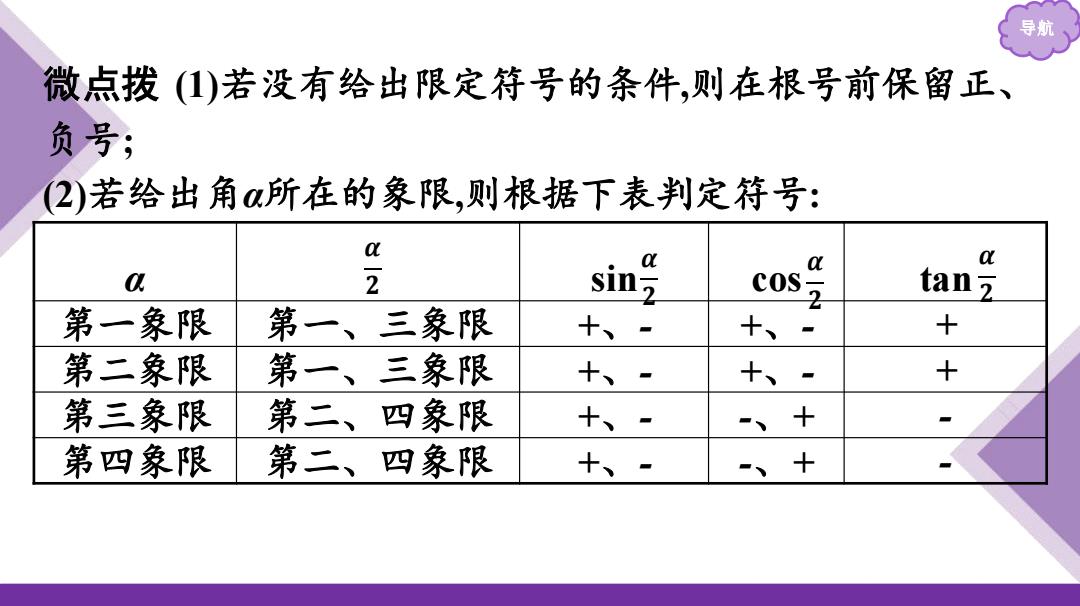
导 微点拨()若没有给出限定符号的条件,则在根号前保留正、 负号; (2)若给出角α所在的象限,则根据下表判定符号: a a a sin c0s tan z 第一象限 第一、三象限 +、- 十、- + 第二象限 第一、三象限 +、- 十、- + 第三象限 第二、四象限 十、- -、十 第四象限 第二、四象限 +、- -、+
导航 微点拨 (1)若没有给出限定符号的条件,则在根号前保留正、 负号; (2)若给出角α所在的象限,则根据下表判定符号: α sin cos tan 第一象限 第一、三象限 +、- +、- + 第二象限 第一、三象限 +、- +、- + 第三象限 第二、四象限 +、- -、+ - 第四象限 第二、四象限 +、- -、+ - 𝜶 𝟐 𝜶 𝟐 𝜶 𝟐 𝜶 𝟐