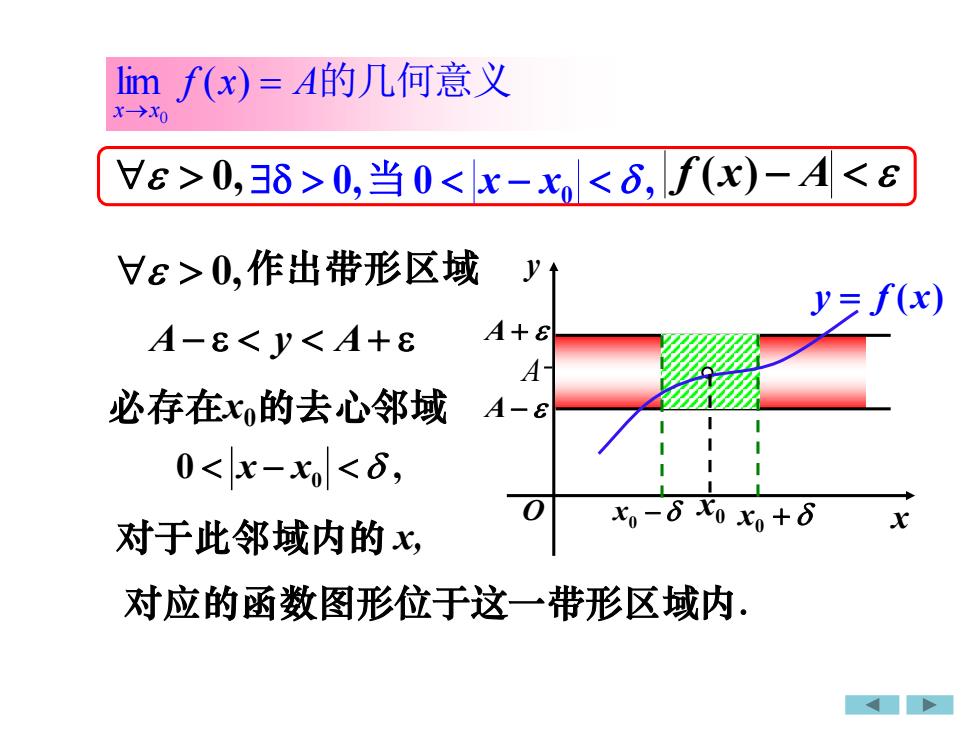
lim f(x)= A的几何意义X-→XoV>0,3>0,当0<x-x<8, f(x)-A<8Vε>0,作出带形区域yy= f(x)A+A-8<Y<A+8A-必存在x的去心邻域A-8--0<x-x|<,-110X- Xo x+8x对于此邻域内的x对应的函数图形位于这一带形区域内
0, A− y A+ 必存在x0的去心邻域 0 , x − x0 对于此邻域内的 x, 对应的函数图形位于这一带形区域内. f x A的几何意义 x x = → lim ( ) 0 作出带形区域 0, 0 , 0,当 x − x0 f (x) − A x y O y = f (x) A− A+ x0 − x0 x0 + A

-般说来,论证lim f(x)=A,应从不等式f(x)-A<ε出发,推导出应小于怎样的正数这个正数就是要找的与8相对应的S,找到S就证明完毕.这个推导常常是困难的但是,注意到我们不需要找最大的S,所以可把 f(x)-A适当放大些,变成易于解出x一x.的式子,找到一个需要的s
一般说来, lim ( ) , 0 f x A x x = → 论证 应从不等式 f (x) − A 出发, 推导出应小于怎样的正数, 这个正数就是要找的与 相对应的 , 这个推导常常是困难的. 但是, 注意到我们不需要找最大的 , 所以 f (x) − A 适当放大些, 的式子, 变成易于解出 x − x0 找到一个需要的 . 找到 就证明完毕. 可把

例1.证明lim C=C(C为常数)x-→>xof(x)-A|=|C-C|=0证:故>0,对任意的>0,当0<|x-xo|<时,总有C-C=0<8lim C = C因此x→>xo
例1. 证明 证: f (x) − A 故 0, 对任意的 0, 当 时 , 因此 总有

lim(2 x -1) = 1例2.证明x-1证 [f(x)-A| =|(2x-1)-1| =2|x-1]>0,欲使|(x)-A|<,只要|x-1<%,取8=%则当 0<|x-1|< 时,必有/2f(x)- A=(2x-1)-1<8因此lim(2 x -1) = 1x->1
例2. 证明 证 = 2 x −1 0, 欲使 取 , 2 = 则当 0 x −1 时 , 必有 因此 只要

例3 证明limx-→1证 函数在点x=1 处没有定义,x-1- 2=x-: f(x)-A:x-1>0,要使|f(x)A<ε,只要取=,当0<x-1<8时,有<8.x-1X:2limx-1x-→1
例3 2. 1 1 lim 2 1 = − − → x x x 证明 证 2 1 1 ( ) 2 − − − − = x x f x A 0, 只要取 = , 当0 x −1 时, 函数在点 = x − 1 f (x) − A , 2 , 1 1 2 − − − x x 有 2. 1 1 lim 2 1 = − − → x x x x = 1 处没有定义. 要使