
第十节闭区间上连续函数的性质最大值(maximum)和-在闭区间上的连续函数有一一些重要的性质这些性质主要应用于分析和论证某些问题时作为理论的根据.这些性质的儿何意义很明显小结思考题
1 第十节 闭区间上连续函数 的性质 介值定理( intermediate value theorem ) 小结 思考题 最大值(maximum )和 最小值(minimum)定理 在闭区间上的连续函数有一些重要的性质, 这些性质主要应用于分析和论证某些问题时作 为理论的根据.这些性质的几何意义很明显

一、最大值和最小值定理定义 设f(x)在区间I上有定义,若存在点EI使得当xEI时,恒有f()≤ f(x)(f (x)≤ f()则称f()为函数f(x)在区间I上的最小(大)值,记为 f()=min f(x)(f()= max f(x)国XE例 y = 1 + sin x,在[0,2元]上, ymax = 2,ymin = 0;y = sgn x,在(-o0,+o0)上, ymax = 1, ymin = -1;在(0,+oo)上, Jmax =Ymin = 1.2
2 定义 f ( ) f ( x) 例 y = sgn x,在(−,+)上, 2, ymax = 1; ymin = − 在(0,+)上, 1. y max = y = 1 + sin x,在[0,2 ]上, 0; ymin = 1, ymax = 设f (x)在区间I上有定义, I, 使得当 x I时, 恒有 若存在点 ( f ( x) f ( )), f ( ) 为函数f(x)在区间I上的最小 值, 记为 则称 f ( ) min f (x) xI = ( f ( ) max f ( x)). xI = (大) y min = 一、最大值和最小值定理
定理1(最大值和最小值定理)在闭区间上连续的函数一定有最大值和最小值若 f(x)EC[a,b]y则, [a,b],使得VxE[a,b],有 f()≥f(x)可ab x51,f(52)≤ f(x)注(1)定理1中的条件“闭区间”和“连续性是不可少的3
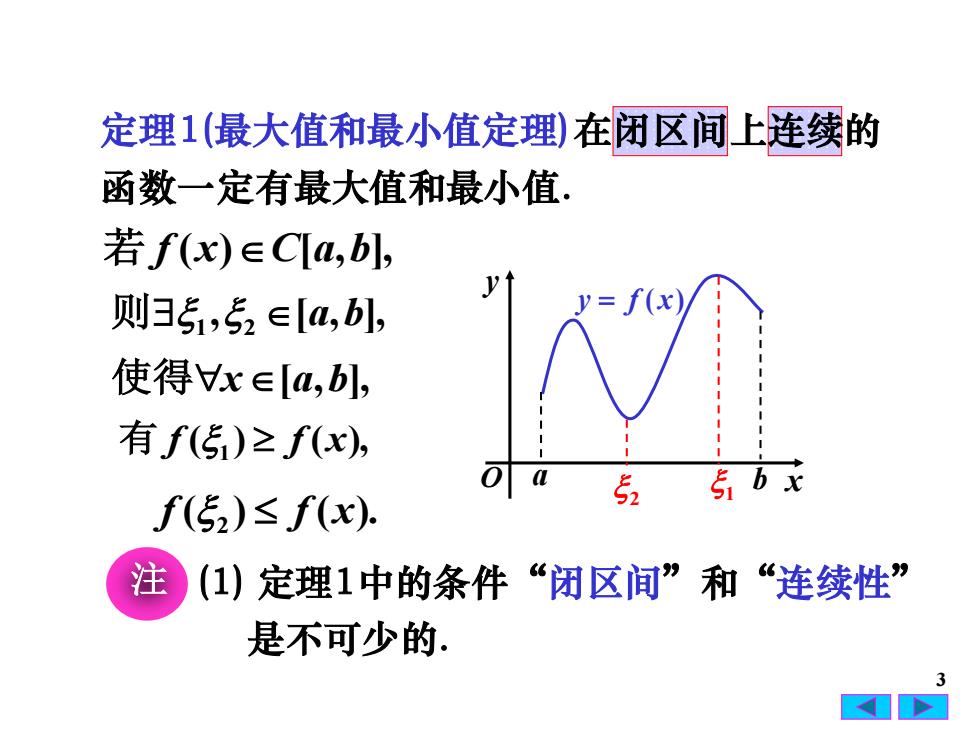
3 在闭区间上连续的 若 f (x)C[a,b], 注 (1) 定理1中的条件“闭区间”和“连续性” 定理1(最大值和最小值定理) 函数一定有最大值和最小值. , [ , ], 则 1 2 a b 使得x[a,b], ( ) ( ), 有 f 1 f x ( ) ( ). f 2 f x 是不可少的. x y O y = f ( x) a b 2 1

如:函数y=x2在开区间(O,1)内连续y=x在(O,1)内没有最大值或最小值。又如:函数yay= f(x)0≤x<1,-x+1,11,y= f(x)=x =1,---x+3, 1<x≤212x在闭区间[0,2]上有间断点x =1,函数f ()在[0,2]上既没有最大值,也没有最小值
4 x y O 1 2 1 在开区间(0,1)内连续, 2 y = x 在(0,1)内 又如: − + = − + = = 3, 1 2 1, 1, 1, 0 1, ( ) x x x x x y f x 在闭区间[0,2]上有 函数f (x)在[0,2]上 既没有最大值, 如: 函数 没有最大值或最小值. 也没有最小值. 间断点 函数 y = f ( x) x = 1, 2 y = x

(2)“闭区间”和“连续性”仅是定理的充分条件而不是必要条件如 函数y=sinx在开区间(0,2元)内连续3元元处但它在x=处取得最大值1;在x=-22取得最小值-1.x, xe[-1,1l,x±0又如 函数f(x)=x=01,在闭区间[-1,1]上有间断点x= 0,但它在x =-1处取得最小值-1;在x=0,1处取得最大值1。5
5 (2) “闭区间”和“连续性” y = sin x 在开区间 (0,2 ) 取得最小值 2 x = 在 处 2 3 x = 函数 = − = 1, 0 , [ 1,1], 0 ( ) x x x x f x 处取得最大值 1. 而不是必要条件. 如 函数 内连续, 但它在 处取得最大值1; −1. 又如 在闭区间 [−1,1] 上有间断点 取得最小值 但它在 x = −1处 − 1; 仅是定理的充分条件, x = 0, 在x = 0,1