《高等数学》课程教学资源（PPT课件）第三章 微分中值定理与导数的应用 3-07 第七节 曲率

曲率第七节弧微分曲率及其计算公式小结曲率圆与曲率半径■小结思考题

第七节 曲 率 ◼ 弧微分 ◼ 曲率及其计算公式小结 ◼ 曲率圆与曲率半径 ◼ 小结 思考题

为了得出曲线y=f（x的曲率公式，先计算弧长函数s对的微分，称为弧微分设函数,f(x)在区间(a, b) y内具有连续导数M基点: M,(xo,yo),M.M(x,y)为任意一点,tXoxx(1)曲线的正向与x增大的方向一致;规定(2)AM = s,当AM 的方向与曲线正向一致时,s取正号，相反时.s取负号

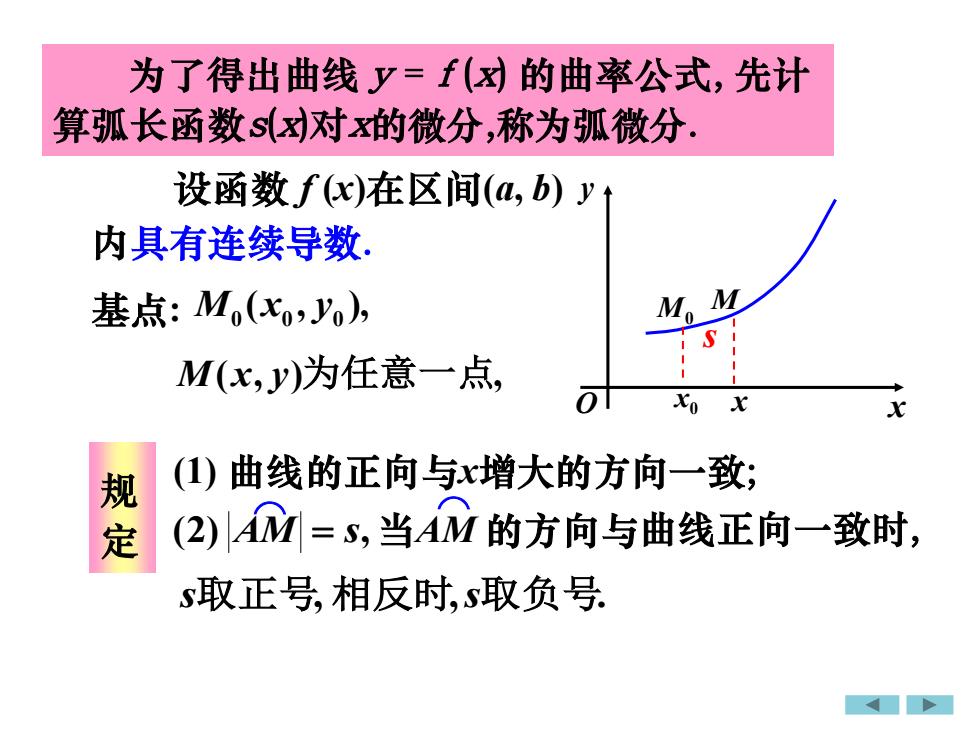
一、弧微分 为了得出曲线 y = f (x) 的曲率公式, 先计 算弧长函数s(x)对x的微分,称为弧微分. ( , ), 0 0 0 M x y M(x, y)为任意一点, (2) AM ⌒ = s, s取正号, 规 定 相反时,s取负号. 设函数 f (x)在区间(a, b) 内具有连续导数. 基点: (1) 曲线的正向与x增大的方向一致; ⌒ 当AM 的方向与曲线正向一致时, x y O s x M 0 x M0

Vs= s(x)是单调增函数M/设M'(x+Ax,y+Ay),如图,Ay4sMM.设对应于x的增量Ax，弧 s4xHS的增量为s,那未tx + 4xXoxxAs= M,M'-M,M =MMIMM"-{MMMM'AS会于是(Ax)AxI MM'IMM(Ax) +(Ay)?()[(会)MM!MM(Ar)

s = s(x) 是单调增函数 . 设M(x + x, y + y), 如图， 设对应于x的增量x, s, s = M M 0 − M0 M = M M 于是  =        2 x s 2         x MM = 2 (x)           2 MM | MM | 2 | MM | 2          = MM | MM | 2 2 2 ( ) ( ) ( ) x x y   +   2          = MM | MM |                  + 2 1 x y 弧 s 的增量为 那末 x y O s x M 0 x M0 x + x M s x y

（））（）M'Ay令Ax→0 取极限,M'→MAsM. MAxISMM即lim=1o1M-→MIMM'x+xXoxxAyds又±/1+y2lim得Ar-→>0Axdx： s= s(x)为单调增函数,故ds= ~1+ y'dx弧微分公式

=   x s 2         x s 2          = MM | MM |                  + 2 1 x y 令x → 0 取极限, M → M,                  +            2 2 1 | | x y MM MM | | | | lim MM MM M M   即 → = 1 又 y x y x =     →0 lim 得 = x s d d d 1 d . 2 故 s = + y x 弧微分公式 2 + 1+ y − s = s(x) 为单调增函数, x y O s x M 0 x M0 x + x M s x y

弧微分公式ds=/1+ydx如将 dx 写到根式内,得ds=/(dx)+(dy)ds = /1 + x'dy如曲线x= x(y),则x = p(t), dx =p'(t)dt如曲线为参数方程y = y(t), dy = yr'(t)dt,ds = p"(t) + y'2(t)dt如曲线以极坐标方程给出 p=p(①)x = p(0)cos0可化为参数方程形式= p()sinO代入公式,得ds = /[p'(0)P +[p(0)Pd

如将 d (d ) (d ) . 2 2 s = x + y 如曲线x = x( y),则 dx = (t)dt, d ( ) ( )d . 2 2 s =  t + t t d 1 d . 2 s = + x y    = =       ( )sin ( )cos y x 代入公式,得 d [ ( )] [ ( )] d . 2 2 s =   +    ds 1 y dx 2 弧微分公式 = +  dy =(t)dt,    = = ( ), ( ), y t x t    = ( ) 可化为参数方程形式 如曲线以极坐标方程给出 如曲线为参数方程 dx 写到根式内,得