
第二节数列的极限数列极限的定义■收敛数列的性质小结思考题
第二节 数列的极限 ◼ 数列极限的定义 ◼ 收敛数列的性质 ◼ 小结 思考题

数列极限的定义一极限概念是从常量到变量,从有限到无限即从初等数学过渡到高等数学的关键极限的思想源远流长庄子(约公元前355~275年)在《天下篇》中写道:“一尺之捶,日取其半,万世不竭?意思是:一尺长的棍子,第一天取其一半,第二天取其剩下的一半,以后每天都取其剩下的一半,这样永远也取不完
一、数列极限的定义 极限概念是从常量到变量,从有限到无限, 即从初等数学过渡到高等数学的关键. 极限的思想源远流长. 庄子(约公元前355~275年)在《天下篇》 “一尺之棰,日取其半,万世不竭”. 意思是:一尺长的棍子,第一天取其一半,第二 天取其剩下的一半,以后每天都取其剩下的一 中写道: 半,这样永远也取不完

“割圆术”中说:刘徽(三世纪)的割之弥细,所失弥少.割之又割,以至不可割,则与圆周合体,而无所失矣意思是:设给定半径为1尺的圆形开始每次把边数加倍,屡次用勾股定理.求出正12边形、正24边形.等等正多边形的边长边数越多,圆内接正多边形越与圆接近,最后与圆周重合,则正多边形周长与圆周长就没有误差了
刘徽(三世纪)的“割圆术”中说: 意思是: 设给定半径为1尺的圆, 形开始,每次把边数加倍,屡次用勾股定理.求出 正12边形、正24边形.等等正多边形的边长, 边数越多,圆内接正多边形越与圆接近,最后与 圆周重合, 则正多边形周长与圆周长就没有误 差了. “割之弥细,所失弥少.割之又割,以至不 可割,则与圆周合体,而无所失矣
正六边形的面积 AR正十二边形的面积 A,正6×2n-1 形的面积A,..SA,A,AA
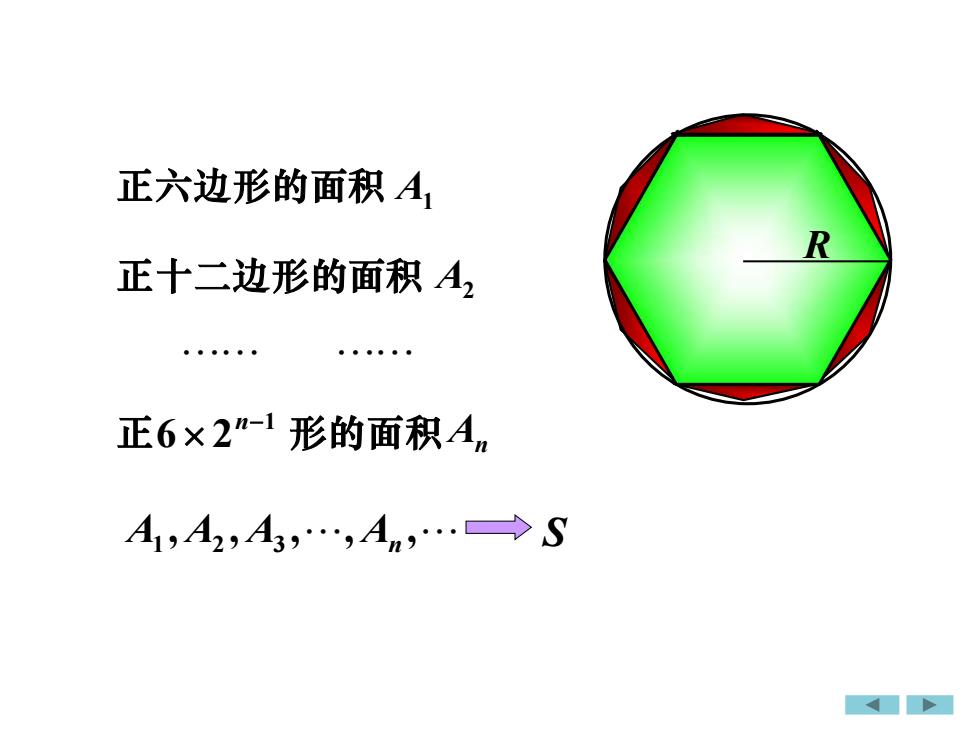
正六边形的面积 A1 正十二边形的面积 A2 正 6 2 n−1 形的面积 An A1 , A2 , A3 , , An , S R

数列的概念定义按照自然数的顺序排列的一列数Xi,X2,...Xn,:简记为{x,},其中x,称为数列x,的通项或者一般项.如[2"]2,4,8,...,2"..n2'4'82
如 2,4,8, ,2 , ; n , ; 2 1 , , 8 1 , 4 1 , 2 1 n {2 } n } 2 1 { n 定义 按照自然数的顺序排列的一列数 x1 , x2 , xn , 简记为 其中xn 称为数列{xn }的 通项 一般项. { }, xn 数列的概念 或者