《高等数学》课程教学资源（PPT课件）第二章 导数与微分 2-05 第五节 函数的微分

第五节函数的微分■微分的定义微分的几何意义1微分公式与运算法则小结思考题

第五节 函数的微分 ◼ 微分的定义 ◼ 微分的几何意义 ◼ 微分公式与运算法则 ◼ 小结 思考题

导数——表示函数在一点处由自变量所引起的函数变化的快慢程度微分——是函数在一点处由于自变量微小变化所引起的改变量的近似值导数与微分个有着密切的联系

导数 微分 导数与微分 表示函数在一点处由自变量所引起 的函数变化的快慢程度. 是函数在一点处由于自变量微小变化 所引起的改变量的近似值. 有着密切的联系

微分的定义一、1.问题的引出实例正方形金属薄片受热后面积的改变量(Ar)XoAx设边长由x.变到x。+△x，LoAxAr：正方形面积 A=x,.. A = (x, + Ax)° - x)XAxxeA=xi= 2x, · Ax + (△x)?(1)(2)要公(1)△x的线性(一次)函数,且为△A的主1当Ax很小时，(2)△x的高阶无穷小,且为△A的次要部很小时可忽略AA~2x.Ar

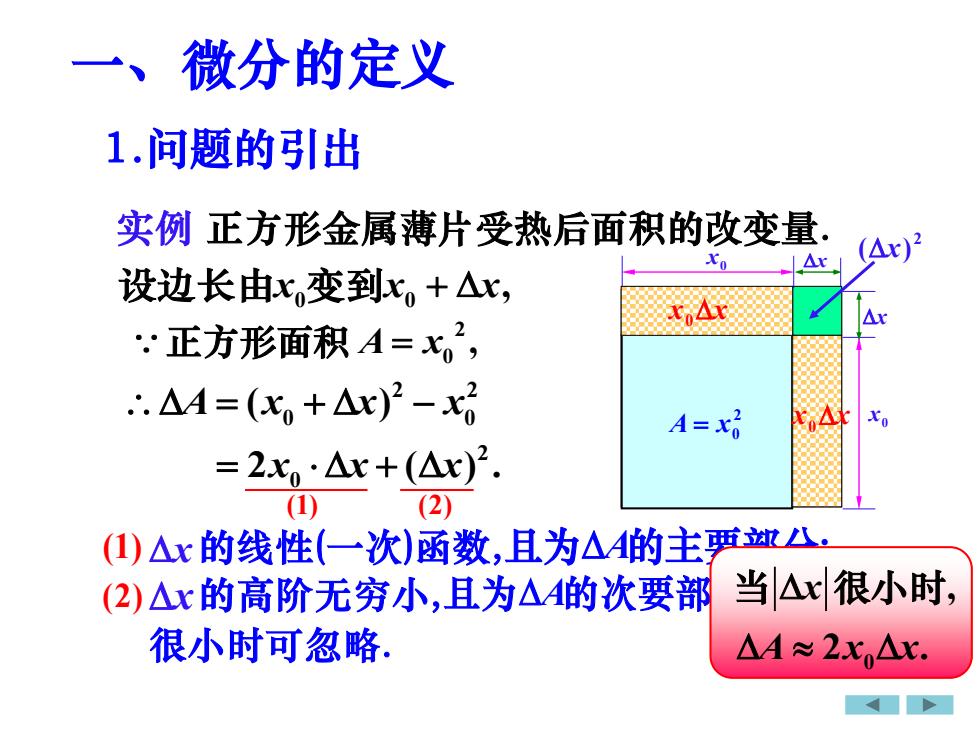
正方形金属薄片受热后面积的改变量. 2 0 A = x x0 0 x 0 0 设边长由x x x 变到 +  , 2 0 正方形面积 A x = , 2 2 0 0  = +  − A x x x ( ) 2 0 =   +  2 ( ) . x x x (1) (2) 且为A的主要部分; x (1) (2) x x 2 (x) 1.问题的引出 实例 x x x 0 x x 0 一、微分的定义 的线性(一次)函数, 且为A的次要部分,当x 很小时可忽略. 0 , 2 . x A x x     的高阶无穷小, 当 很小时

再如，设函数y=x3在点x,处的改变量为△x时求函数的改变量△yAy =(xo + Ax) - xi3x) . Ax/+ 3x, :(Ax)? +(Ax)3.(1)(2)当△x很小时,(2)是△x的高阶无穷小o(△x),:. 4y ~ 3xi : 4x.既容易计算文是较好的近似值

再如, 3 0 设函数 y x x x =  在点 处的改变量为 时, 3 0 3 0 y = (x + x) − x 3 3 ( ) ( ) . 2 3 0 2 = x0  x + x  x + x (1) (2) 当 x 很小时,  y  (2) ( ), 是  x o x 的高阶无穷小 既容易计算又是较好的近似值 求函数的改变量y. 3 . 2 0 x  x

对一般函数y= f(x),如果y= f(x)满足一定条件，则函数的增量4可以表示为Ay = A△x + o(△x)其中A是不依赖于△r的常数，因此A△r是A的线性函数，且它与△V之差Ay - AAx =0(△x)Ax ~ △y当A￥0,且△x很小时对一般函数y=f(x),如果存在这样的近似公式，则无论在理论分析上还是在实际应用中都是十分重要的

对一般函数y f x = ( ), 其中A x 是不依赖于 的常数, y = Ax 当A  0, Ax  y 如果y f x = ( )满足 一定条件, y 因此A x x   是 的 线性函数, 且它与y之差 对一般函数 则无论在理论分析上还是在实际 + o(x). 则函数的增量 可以表示为 如果存在这样的 近似公式, 应用中都是十分重要的. o(x) 且 x 很小时, y = f (x), y − Ax =