
第一节导数的概念引例导数定义导数的几何意义可导与连续的关系小结
◼ 引例 ◼ 导数定义 ◼ 导数的几何意义 ◼ 可导与连续的关系 ◼ 小结 第一节 导数的概念

引例一例1直线运动的瞬时速度问题一质点作直线运动,已知路程S与时间t的关系 s = s(t).试确定tO时的瞬时速度v(tO)解从时刻→+△质点走过的路程As = s(t + △t) - s(to),As这段时间内的平均速度(△t)△t若运动是匀速的,平均速度就等于质点在每个时刻的速度
例1 直线运动的瞬时速度问题 一质点作直线运动,已知路程 s 与时间 t 的 试确定t0时的瞬时速度v(t0). ( ) ( ), 0 0 s = s t + t − s t 这段时间内的平均速度 v(t) 在每个时刻的速度. 解 . t s = 若运动是匀速的,平均速度就等于质点 关系 s = s(t). 质点走过的路程 一、引例 , 0 0 从时刻 t → t + t

若运动是非匀速的,平均速度△t)是这段时间内运动快慢的平均值,△ 越小它越近似的表明to时运动的快慢.因此,人们把to时的速度定义为Ass(to +△t)-s(to)limv(fo) = lim AtAtt-→0并称之为t时的瞬时速度t)注此式既是它的定义式,文指明了它的计算方法,瞬时速度是路程对时间的变化率
此式既是它的定义式,又指明了它的计算 它越近似的 定义为 v(t 0 ) = , ( ) ( ) lim 0 0 0 t s t t s t t + − = → 并称之为t0时的瞬时速度v(t0 ). 瞬时速度是路程对时间的变化率. 若运动是非匀速的,平均速度 v(t) 是这段 时间内运动快慢的平均值, t 越小, 表明 t0 时运动的快慢.因此, 人们把 t0时的速度 注 方法, t s 0 lim Dt®

例2曲线的切线斜率问题若已知平面曲线y=f(x),如何作过曲线上点M.(xo,f(x的切线呢初等数学中并没有给出曲线切线的定义我们知道与圆周有唯一交点的直线即为圆周过该点的切线.但此定义不适应其它曲线.如与抛物线有唯一交点的直线不一定是切线对于一般曲线如何定义其切线呢?法国数学家费马在1629年提出了如下的定义和求法,从而圆满地解决了这个问题切线位置割线的极限位置
例2 割线的极限位置—— 对于一般曲线如何定义其切线呢? 曲线的切线斜率问题 若已知平面曲线 y = f (x), ( , ( )) 0 0 x0 M x f 如何作过 的切线呢. 初等数学中并没有给出曲线切线的定义. 过该点的切线. 我们知道与圆周有唯一交点的直线即为圆周 但此定义不适应其它曲线. 如 与抛物线有唯一交点的直线不一定是切线. 切线位置. 曲线上点 法国 数学家费马在1629年提出了如下的定义和求 法,从而圆满地解决了这个问题
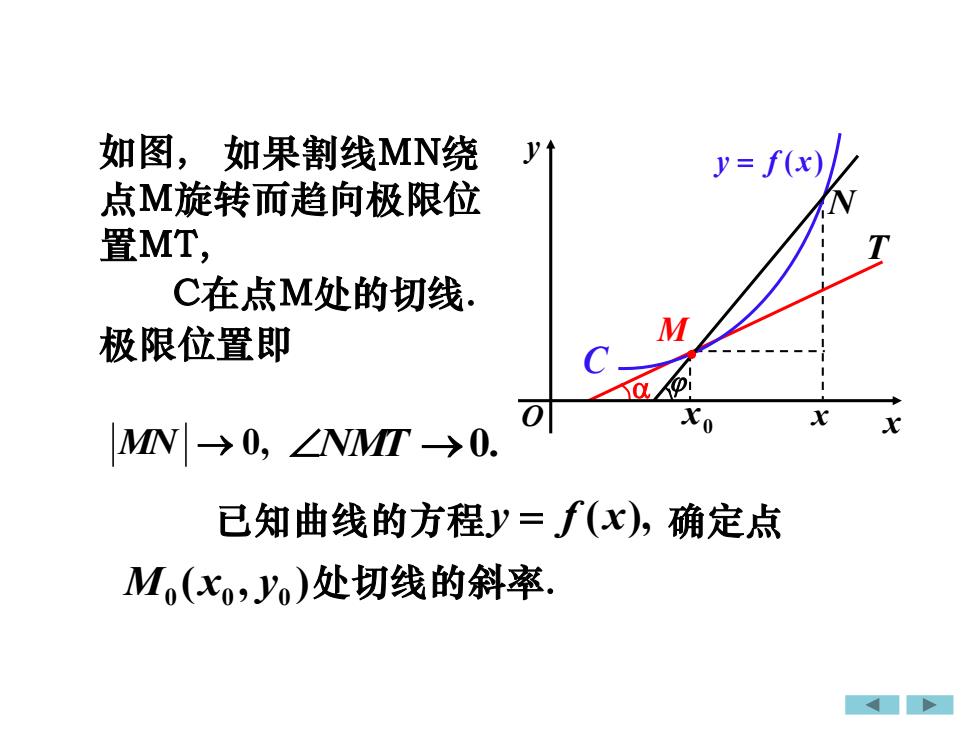
如图,如果割线MN绕Vy= f(x)点M旋转而趋向极限位置MT,TC在点M处的切线M极限位置即C@laxoxxMN|-→0, ZNMT →0.已知曲线的方程y=f(x),确定点M.(xo,Jo)处切线的斜率
x0 ( , ) 处切线的斜率. 0 0 0 M x y 已知曲线的方程 确定点 如果割线MN绕 点M旋转而趋向极限位 置MT, 极限位置即 MN → 0, C在点M处的切线. 如图, NMT →0. y = f (x), x T x y O y = f ( x) C N • M