
第八节函数的连续性与间断点函数的连续函数的间断点小结思考题
1 第八节 函数的连续性与间断点 ◼ 函数的连续 ◼ 函数的间断点 ◼ 小结 思考题

在自然界中,许多事物的变化是连续的,如气温变化很小时,单摆摆长变化也很小。时间变化很小时,生物生长的也很少。这种现象在函数关系上的反映就是函数的连续性。在高等数学中,主要的研究对象就是连续函数。从直观上不妨这样说,连续函数的特征就是它的图形是连续的,也就是说,可以一笔画成
在自然界中,许多事物的变化是连续的,如 气温变化很小时,单摆摆长变化也很小。时间 变化很小时,生物生长的也很少。这种现象在 函数关系上的反映就是函数的连续性。在高等 数学中,主要的研究对象就是连续函数。从直 观上不妨这样说,连续函数的特征就是它的图 形是连续的,也就是说,可以一笔画成
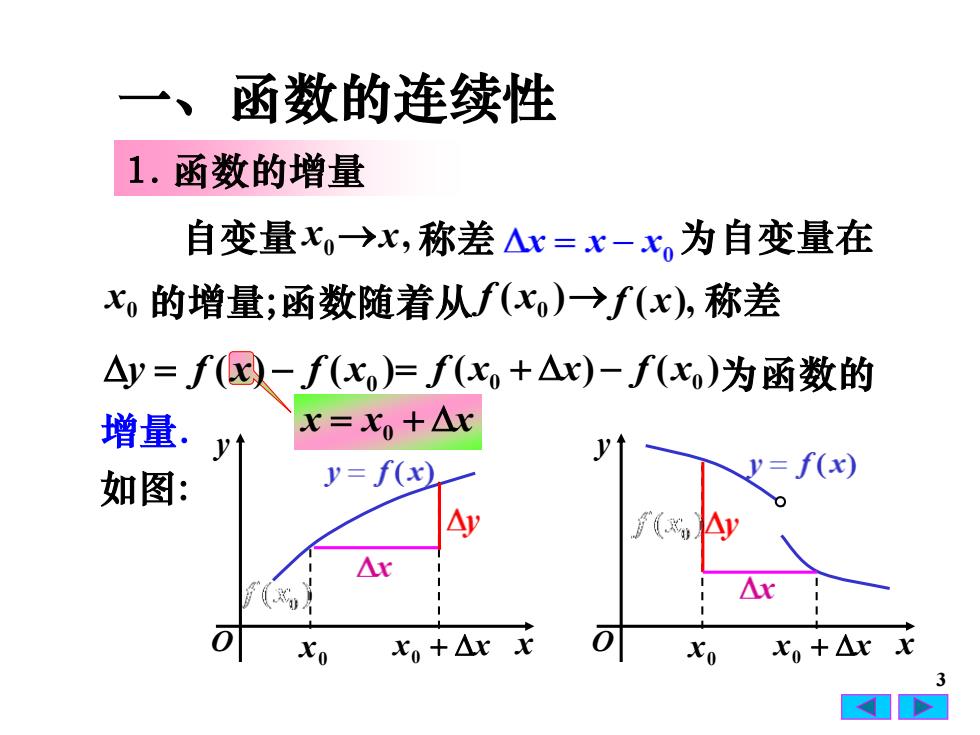
一、函数的连续性1.函数的增量自变量Xo→x,称差△x= x-x为自变量在xo的增量;函数随着从f(xo)→f(x),称差Ay=f(x)f(x)=f(x+△x)-f(xo)为函数的x=x.+Ar增量.VV=f(x)y=f(x)如图:AyAyArAx可可Xo + Ax xXo+Ar xxoxo3公
3 1. 函数的增量 ( ) ( ) x0 y = f x − f 自变量 0 x →x, 称差 为自变量在 0 x 的增量;函数随着从 ( ) x0 f →f ( x), 称差 ( ) ( ) 0 x0 = f x + x − f 为函数的 增量. 如图: x = x0 + x 一、函数的连续性 x y O x y O 0 x x0 + x 0 x x0 + x
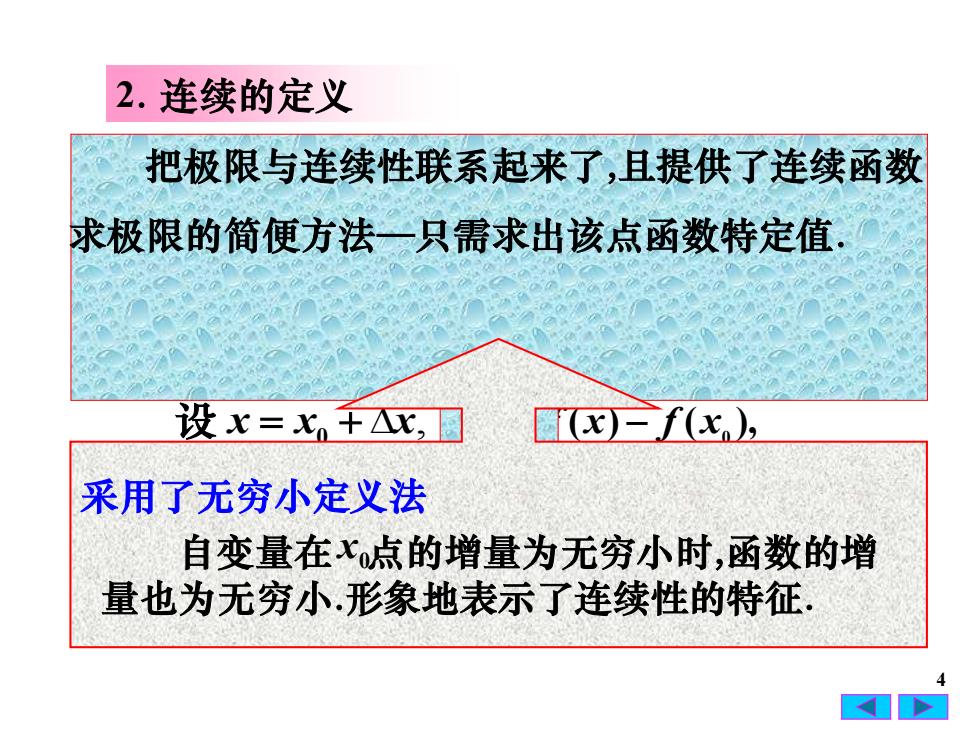
2.连续的定义把极限与连续性联系起来了,且提供了连续函数求极限的简便方法一一只需求出该点函数特定值设x=x.+x(x)-f(x),采用了无穷小定义法自变量在x点的增量为无穷小时,函数的增量也为无穷小.形象地表示了连续性的特征
则称函数 在 处 0 x f (x) f (x) f (x) x0 f x( ) 0 x 4 连续, 2. 连续的定义 , 0 设 x x x = + ( ) ( ), x0 y = f x − f x → 0 定义1 设函数 在 ( ) U x0 内有定义,若 lim 0 0 = → y x 则称函数 在 处 并称 为函数 的 连续点. y → 0 定义2 若 lim ( ) ( ), 0 0 f x f x x x = → 连续. 充分必要条件 把极限与连续性联系起来了,且提供了连续函数 求极限的简便方法—只需求出该点函数特定值. 自变量在 点的增量为无穷小时,函数的增 量也为无穷小.形象地表示了连续性的特征. 采用了无穷小定义法 x0

定义3(-)>0,>0,使当xxl<时,恒有f(x)-f(x)<把极限定义严密化,便于分析论证连续性的三种定义形式不同,但本质相同这三种定义中都含有三个要素:(1) f(x)在U。(x)内有定义;(2) lim f(x)存在;x→x(3) lim f(x) = f(xo)x→xo5A
5 连续性的三种定义形式不同,但本质相同. 这三种定义中都含有三个要素: f (x)在 ( ) (1) U x0 内有定义; lim ( ) 0 f x x→x (2) lim ( ) 0 f x x→x (3) ( ) x0 = f 把极限定义严密化,便于分析论证. 存在; 定义3 ( − ) 0 , , 使 当 x − x0 时 0 , ( ) ( ) . 0 恒 有 f x − f x