
第三章微分中值定理与导数的应用习题课>教学要求>典型例题
第三章 微分中值定理与导数的应用 ➢教学要求 ➢典型例题 习 题 课

一、教学要求1:理解罗尔(Rolle)定理和拉格朗日(Lagrange定理2.了解柯西(Cauchy)定理和泰勒(Tayloy)定理3.理解函数的极值概念,掌握用导数判断函数的单调性和求极值的方法
1. 理解罗尔(Rolle) 定理和拉格朗日(Lagrange) 定理. 2. 了解柯西(Cauchy)定理和泰勒(Tayloy)定理. 3. 理解函数的极值概念,掌握用导数判断函数 的单调性和求极值的方法. 一、教学要求

4.会用导数判断函数图形的凹凸性,会求拐点,会描绘函数的图形(包括水平,铅直和斜渐近线).会求解最大值和最小值的应用问题5.会用洛必达(L,Hospital)法则求不定式的极限6.了解曲率和曲率半径的概念并会计算曲率和曲率半径
4. 会用导数判断函数图形的凹凸性,会求拐点,会描 绘函数的图形(包括水平,铅直和斜渐近线).会求 解最大值和最小值的应用问题. 5. 会用洛必达(L,Hospital)法则求不定式的极限. 6. 了解曲率和曲率半径的概念并会计算曲率和曲 率半径
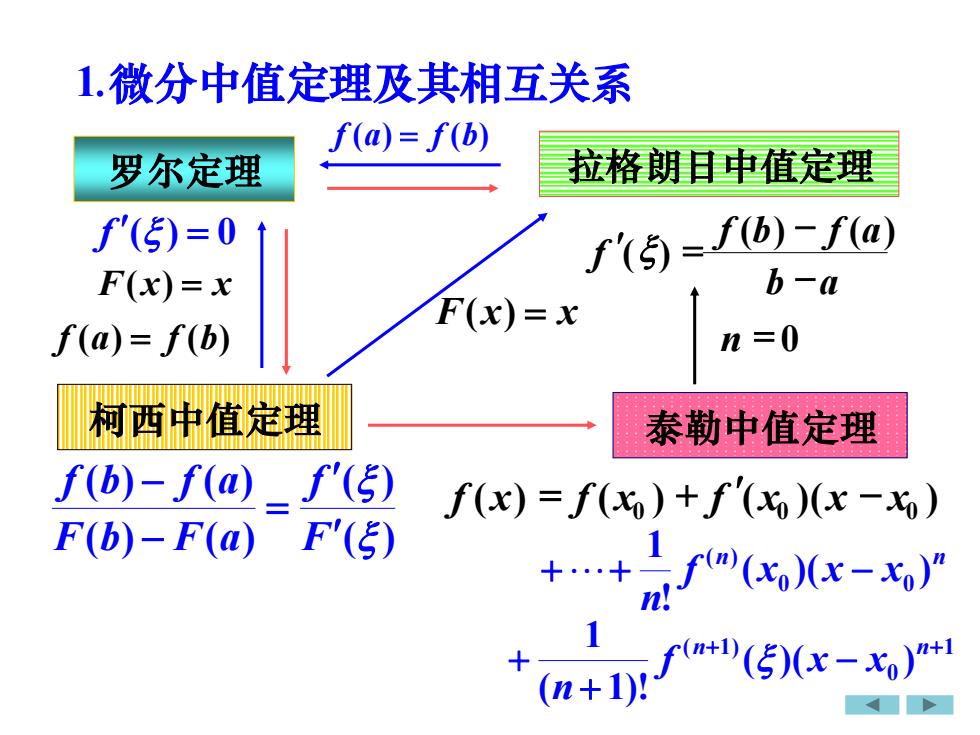
1.微分中值定理及其相互关系f(a) = f(b)拉格朗日中值定理罗尔定理F(5) =f(b)-f(α)f()=0b-aF(x)= xF(x)= xn=0f(a) = f(b)柯西中值定理泰勒中值定理f(b)-f(a) - f(E)f(x) = f(xo) + f(x)(x -xo)F(b)-F(a)F'()f(n)(x,)(x -xo)"(5)(x -xo)"+1n+
f (a) = f (b) 1.微分中值定理及其相互关系 罗尔定理 f ( ) = 0 ( ) ( ) ( ) ( ) ( ) ( ) F f F b F a f b f a = − − 拉格朗日中值定理 ( ) ( ) ( ) f a f b F x x = = 柯西中值定理 F(x) = x 泰勒中值定理 1 0 ( 1) ( )( ) ( 1)! 1 + + − + + n n f x x n n n f x x x n ( )( ) ! 1 0 0 ( ) ++ − ( ) ( ) ( )( ) 0 x0 x x0 f x = f x + f − b a f b f a f − − = ( ) ( ) () n = 0

2.微分中值定理的主要应用(1)研究函数或导数的性态(2)证明方程根的存在性(3)证明恒等式或不等式(4)证明有关中值问题的结论
2. 微分中值定理的主要应用 (1) 研究函数或导数的性态 (3) 证明恒等式或不等式 (4) 证明有关中值问题的结论 (2) 证明方程根的存在性