
第四节函数的单调性与曲线的凹凸性函数单调性的判别法单调区间求法曲线凹凸性的判别法曲线的拐点及其求法■小结思考题
第四节 函数的单调性与 曲线的凹凸性 ◼ 函数单调性的判别法 ◼ 单调区间求法 ◼ 曲线凹凸性的判别法 ◼ 曲线的拐点及其求法 ◼ 小结 思考题
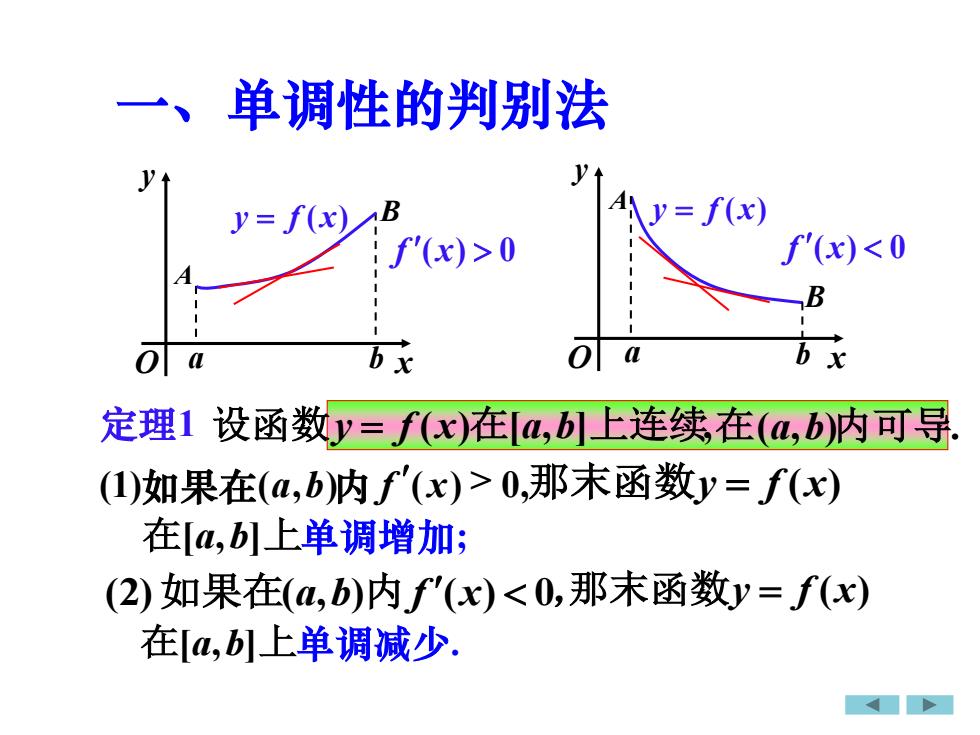
单调性的判别法一、1Ly.ANy= f(x)y= f(x) Bf'(x)<0 f'(x)>0AB--可ab xolb xa定理1设函数y=f(x)在[a,bl上连续在(a,b)内可导(1)如果在(a,b)内f'(x)>0,那末函数y= f(x)在[a,b]上单调增加;(2)如果在(a,b)内,f'(x)<0,那末函数y= f(x)在[a,b]上单调减少
f (x) 0 f (x) 0 定理1 在(a,b)内可导. (2)如果在(a,b)内f (x) 0, 那末函数y = f (x) 在[a,b]上 那末函数y = f (x) 在[a,b]上 单调增加; 单调减少. 一、单调性的判别法 x y O a b A y = f (x) B x y O y = f (x) a b A B 设函数y = f (x)在[a,b]上连续, (1) ( , ) ( ) > 0, 如果在 a b 内 f x

证 V xj,x, E[a,b],且x <x,拉氏定理f(x2)-f(x)= f()(x2 -x) (x, <≤<x)(1)若在(a,b)内,f'(x) >0,则 f'() >0,:. f(x2)>f(x),: y= f(x)在a,b上单调增加(2)若在(a,b)内,f'(x)<0,则 f'()<0,. f(x2)<f(x),. y= f(x)在[a,b]上单调减少注此定理不论对于开、闭、有限或无穷区间都正确
证 , [ , ], x1 x2 a b , 且 x1 x2 拉氏定理 ( ) ( ) ( )( ) 2 1 x2 x1 f x − f x = f − 若在(a,b)内, 则 f ( ) 0, ( ) ( ), 2 x1 f x f y = f (x)在[a,b]上单调增加; 若在(a,b)内, 则 f ( ) 0, ( ) ( ), 2 x1 f x f y = f (x)在[a,b]上单调减少. ( ) x1 x2 f (x) 0, f (x) 0, (1) (2) 此定理不论对于开、闭、有限或无穷 区间都正确. 注

例 讨论函数y=e-x-1的单调性解 定义域为(-80,+80):y'=e*-l.在(-80,0)内, y'<0,:函数在一8,0单调减少;在(0,+8)内, J' >0,:函数在0,+8)单调增加
例 解 讨论函数y = e − x − 1的单调性. x = − 1. x y e 在(−,0)内, y 0, 函数在(− ,0]单调减少; 在(0,+)内, y 0, 函数在[0,+ )单调增加. 定义域为 (−,+)

二、单调区间求法问题如上例,函数在定义区间上不是单调的但在各个部分区间上单调。定义若函数在其定义域的某个区间内是单调的则该区间称为函数的单调区间导数等于零的点和不可导点,可能是单调区间的分界点.方法用方程f(x)=0的根及f(x)不存在的点划分函数f(x)的定义区间然后判定区间内导数的符号
方法 用方程 f (x) = 0的根及 f (x)不存在的点 问题 如上例, 函数在定义区间上不是单调的, 定义 若函数在其定义域的某个区间内是单调的, 划分函数f (x)的定义区间, 然后判定区间内导数 的符号. 的分界点. 二、单调区间求法 但在各个部分区间上单调. 则该区间称为函数的单调区间. 导数等于零的点和不可导点,可能是单调区间