§7.3数量积、向量积、混合积 数量积 向量积 主要内容 平行垂直 混合积 的条件 坐标表示
§7.3 数量积、向量积、混合积 坐标表示 主要内容 混合积 数量积 向量积 平行垂直 的条件

两向量的数量积 定义:两向量a与的模和它们 性质(1)aa=d=a2 夹角的余弦的乘积叫做 (2)当a=0或b=0时 两向量a和的数量积.记做 a.b=0 a.6或ab 当ā≠0,五≠0时 a.b=lacos.∠(a,) a.b=dPrjb=bPrjga i.i=j.j=k.k=1 (3)a.b=0⊙a1b i.j=i.k=j.k=0
一、 两向量的数量积 定义:两向量 a 与 b 的模和它们 夹角的余弦的乘积叫做 两向量a 和b 的数量积. 记做 a b 或 ab a b a b a b cos ( , ) 性质(1) 2 2 a a a a i i j j k k 1 (3) a b a b 0 i j i k j k 0 (2)当 a 0或b 0时 当 a b 0, 0 时 a b a j b b j a a b Pr Pr a b 0

一 两向量的数量积 b-a=acos-∠(6,d←☐定义→a:6=la6lcos∠(a,b) ∠(a,b)=∠(b,a) a.b=b.a (a+b)c=0 (a+b)-c=cPrjg(a+b) ac=0,b.c=0 c=0 对于c c≠0 和的投影等 (a+b)c=0 (a+b).c=cPrja+cPrjb a.c+b.c=0 于投影之和 (a+b).c=a.c+b.c
一、 两向量的数量积 定义 a b a b a b cos , b a b a b a cos , a b b a , , a b b a 对于c c 0 c 0 ( ) 0 0, 0 a b c a c b c (a b) c c Pr j (a b) c a b c c j c a c j c b ( ) Pr Pr ( ) 0 0 a b c a c b c a b c a c b c ( ) 和的投影等 于投影之和
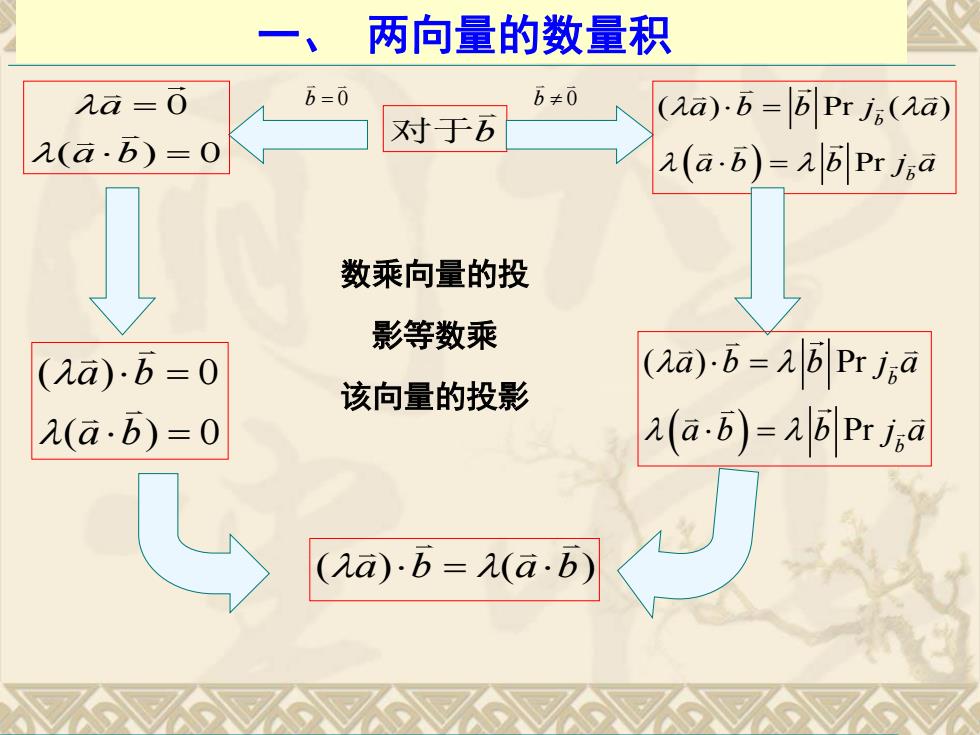
两向量的数量积 λa=0 6=0 6≠0 对于五 (Aa).B=B Prj;(Aa) 入(a.b)=0 A(a.B)=BPri;a 数乘向量的投 影等数乘 (a)b=0 (Aa).B=BPrjja 该向量的投影 (a.b)=0 A(a-B)=1BPrJa (a)-b=(a.b)
一、 两向量的数量积 对于b b 0 b 0 0 ( ) 0 a a b ( ) Pr ( ) Pr b b a b b j a a b b j a ( ) Pr Pr b b a b b j a a b b j a ( ) 0 ( ) 0 a b a b ( ) ( ) a b a b 数乘向量的投 影等数乘 该向量的投影

一、两向量的数量积 数量积运算规律与数量乘法运算规律的比较 (1)交换律a.b=b.a (1)交换律a·b=b·a (2) 关于数因子的结合律 (2) 结合律 (a)b=2(a.b)=a(2b) (2a)b=(ab)=a(b) (3)分配律 (3)分配律 (a+b).c=a.c+b.c (a+b)c=ac+b·C (4)(ab)c=a(bc)一般不成立 (4)(ab)c=a(be) (5)a记=bc,c≠0推不出a=b. (5)ac=bc,c≠0必有a=b
数量积运算规律与数量乘法运算规律的比较 一、两向量的数量积 (1)交换律 a b b a (2) 关于数因子的结合律 ( a) b (a b) a ( b) (3)分配律 a b c a c b c ( ) (4) (ab)c a(bc) 一般不成立 (5)ac bc c , 0 推不出a b . (1)交换律 a b b a (2) 结合律 ( ) ( ) ( ) a b a b a b (3)分配律 ( ) a b c a c b c (4) ( ) ( ) ab c a bc (5)ac bc c , 0必有a b