
第五章 定积分及其应用 主要内容: 一、定积分的概念与性质 二、微积分基本公式 三、定积分的求法 四、定积分的应用
第五章 定积分及其应用 主要内容: 一、定积分的概念与性质 二、微积分基本公式 三、定积分的求法 四、定积分的应用
§5.1 定积分的概念与性质 定积分的 定义 问题的提出 定积分的 主要内容 几何意义 定积分的 性质 定积分的 应用
主要内容 问题的提出 定积分的 定义 定积分的 性质 定积分的 几何意义 定积分的 应用 §5.1 定积分的概念与性质 5.1
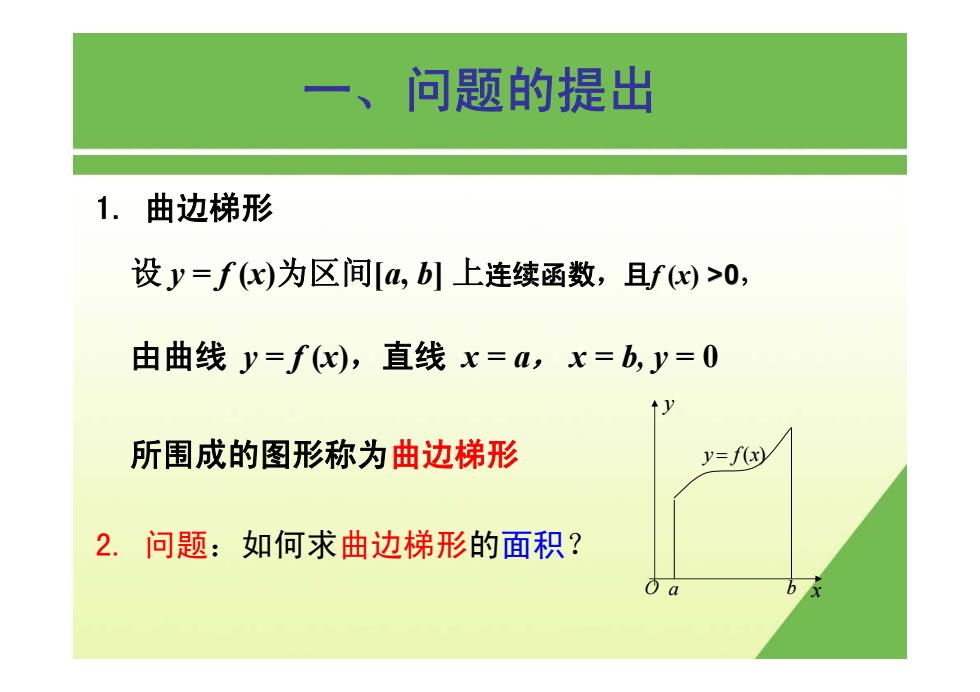
一、问题的提出 1.曲边梯形 设y=f(x)为区间,b]上连续函数,且f)>0, 由曲线y=fx),直线x=,x=b,y=0 所围成的图形称为曲边梯形 y=f(x) 2.问题:如何求曲边梯形的面积? 0 a
一、问题的提出 1. 曲边梯形 设 y = f (x)为区间[a, b] 上连续函数,且f (x) >0, 由曲线 y = f (x),直线 x = a, x = b, y = 0 所围成的图形称为曲边梯形 2. 问题:如何求曲边梯形的面积? x y O a b y = f(x)
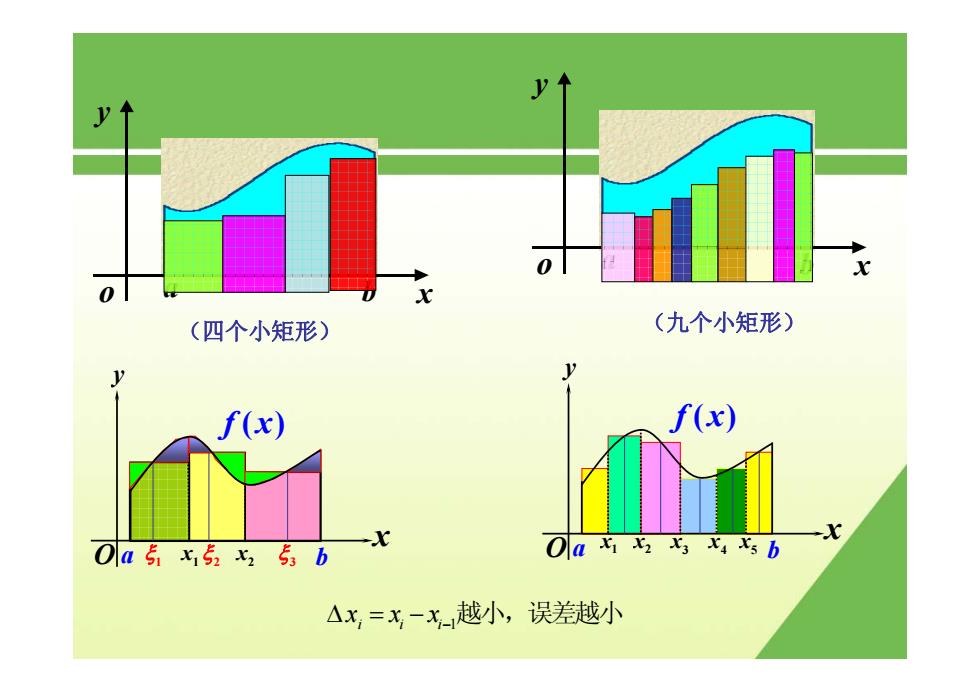
0 (四个小矩形) (九个小矩形) f(x) f(x) Oa5x5x2 5 b Oax x2 x3 Xsxs b △x,=X一x越小,误差越小
a b x y o (四个小矩形) a b x y o (九个小矩形) x y O a b f ( ) x 1 x 1 ξ 2 x 2 ξ 3 ξ x y O a b f ( ) x 1 x 5 x2 x 3 x 4 x i ii 1 x xx Δ = − − 越小,误差越小
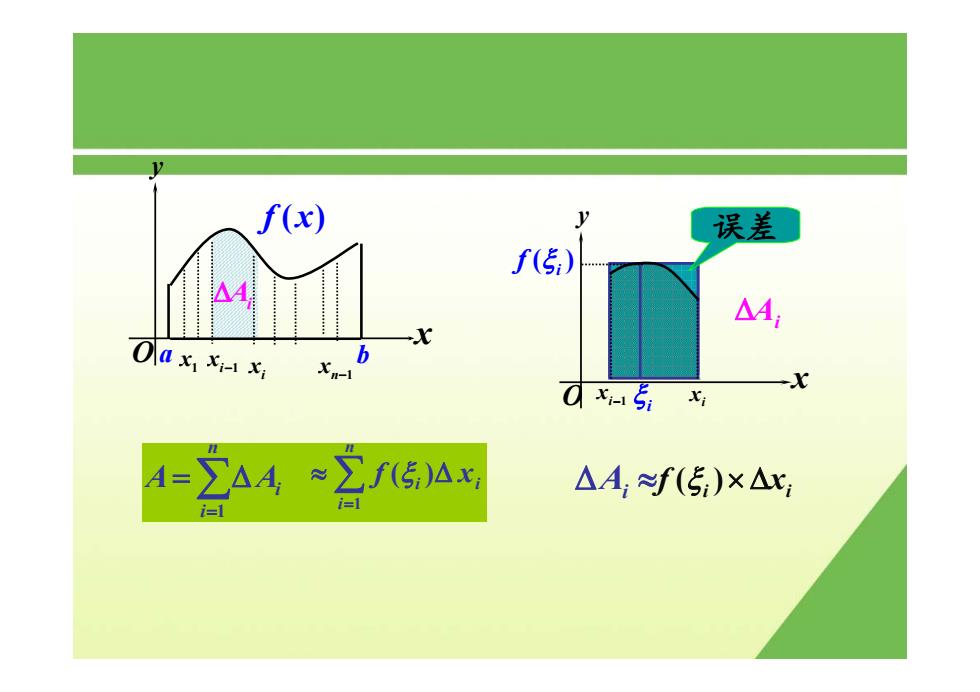
f(x) y 误差 f(5) △4 △4 Oaxxixi 七,b 0x15i9 A=2A4=25)A △A:≈f(5:)×△x
x y O a b f x( ) 1 x n x −1 i 1 x − i x x y O i 1 x − i x i ξ ( )i f ξ ( )i i f x ξ × Δ 误差 ΔAi ∑ = = Δ n i A Ai 1 ΔAi ≈ ΔAi ∑ = ≈ Δ n i i xi f 1 (ξ )