
第四章 不定积分 主要内容: 一、不定积分的概念与性质 二、换元积分法 三、分部积分法 四、有理函数的积分 五、积分表的使用
第四章 不定积分 一、不定积分的概念与性质 二、换元积分 法 三、分部积分法 四、有理函数的积分 五、积分表的使用 主要内容 :
§4.1不定积分的概念与性质 不定积分的概念 原函数的概念 不定积分 主要内容 的性质 基本积分表 不定积分的 基本求法
§4.1 不定积分的概念与性质 主要内容 不定积分的概念 原函数的概念 基本积分表 不定积分 的性质 不定积分的 基本求法

一、原函数与不定积分的概念 1.原函数 (1)定义:如果对任意的x∈1,都有 F(x)=f(x)(dF(x)=f(x)dx) 则称函数F(x)是f(x)(或f'(x)d)区间I上的一个原函数. 原函数必需 可导 anti-derivative
(1)定义:如果对任意的x I ∈ ,都有 F′() () x fx = (或dF x f x dx () () = ′ ) 则称函数 F(x)是 f ( ) x (或 f x dx ′( ) )区间 I 上的一个原函数. 1. 原函数 一、原函数与不定积分的概念 anti-derivative 原函数必需 可导

一、原函数与不定积分的概念 例1.下列函数中可以作为某些函数在(-0,+∞)上的原函数的是() A:F(x)= B:F(x)=x3 x'sin- x≠0 C:F(x)=sgnx D:F(x)= 0, x=0 (sin- E:F(x)=sinx x≠0 F: F(x 0. x=0
一、原函数与不定积分的概念 例 1. 下列函数中可以作为某些函数在(,) −∞ +∞ 上的原函数的是( ) A: Fx x ( ) = B: 2 3 Fx x ( ) = C: F( ) sgn x x = D: 2 1 sin , 0 ( ) 0, 0 x x F x x x ⎧ ⎪ ≠ = ⎨ ⎪ ⎩ = E: Fx x ( ) sin = F: 1 sin , 0 ( ) 0, 0 x x F x x x ⎧ ⎪ ≠ = ⎨ ⎪ ⎩ =
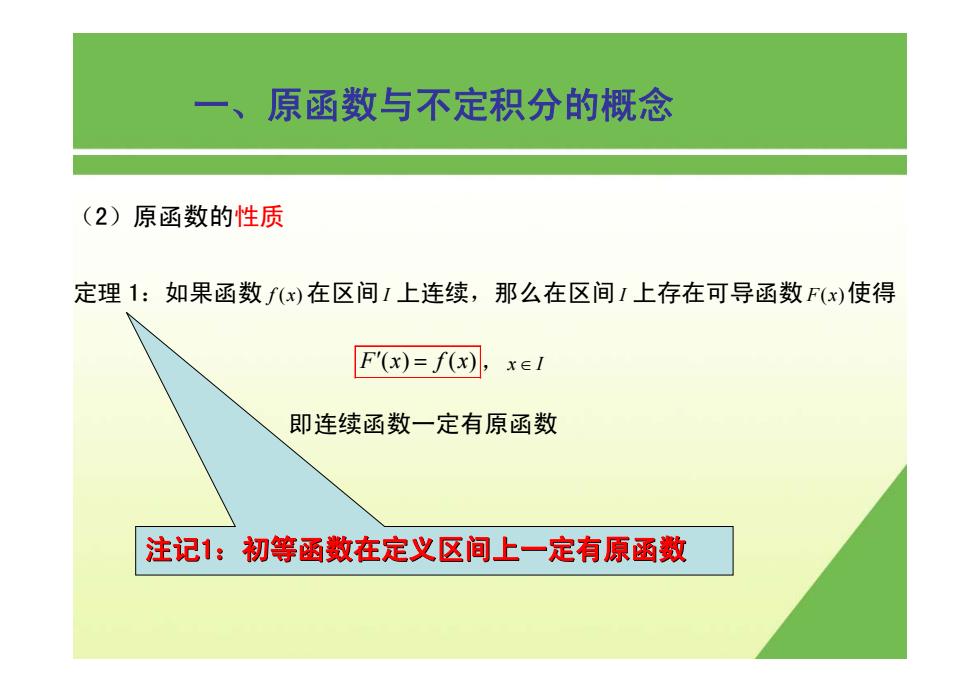
一、原函数与不定积分的概念 (2)原函数的性质 定理1:如果函数f(x)在区间1上连续,那么在区间1上存在可导函数F(x)使得 F(x)=f(x), 即连续函数一定有原函数 注记1:初等函数在定义区间上一定有原函数
(2)原函数的性质 定理 1:如果函数 f x( )在区间I 上连续,那么在区间I 上存在可导函数F x( )使得 F′() () x fx = , x I ∈ 即连续函数一定有原函数 一、原函数与不定积分的概念 注记1:初等函数在定义区间上一定有原函数