南阳师范学院：《高等数学》课程教学资源（课件讲稿）第七章 向量代数与空间解析几何 §7.5 空间直线及其方程

§7.5 空间直线及其方程 空间曲线 空间直线方 空间直线与平 空间直线与空 程 面的夹角 间直线的夹角 Oeo①0⊙8

机动 目录 上页 下页 返回 结束 空间曲线 空间直线方 程 空间直线与平 面的夹角 空间直线与空 间直线的夹角 §7.5 空间直线及其方程

一、 空间曲线方程 空间曲线在空间解析几何中被看成是点的几何轨迹， 设曲面S:F(x,y,)=0与曲面S2:G(x,y,)=0相交于曲线C.则 ①曲线C上的任意点的坐标满足方程组 F(x,v,=)=0, (2) G(x,y,z)=0 ②满足方程组(2)的点都在曲线0 称方程组(2)为空间曲线C的一般方程，称曲线C为方程组(2)的图形 注记：空间直线L总可以看作是两平面的交线，因此求空间直线的方程 关键是找出过该直线的两平面的方程

一、空间曲线方程 空间曲线在空间解析几何中被看成是点的几何轨迹． 设曲面S:1 F x y z  , , 0   与曲面S:2 G , , 0  x y z  相交于曲线C .则 ①曲线C 上的任意点的坐标满足方程组     , , 0, G , , 0 F x y z x y z       （2） ②满足方程组（2）的点都在曲线 C 称方程组（2）为空间曲线C 的一般方程，称曲线C 为方程组（2）的图形. 注记 1：空间直线 L总可以看作是两平面的交线，因此求空间直线的方程 关键是找出过该直线的两平面的方程

二、空间直线的一般方程 设空间直线L为两平面 Ax+By+Cz+D=0 (1) Ax+B2y+C2z+D=0 Π1：Ax+By+C1z+D=0 称方程组(1)为直线L的一般方程 Π2：A2x+B2y+Cz+D,=0 注记2：x,y,z轴的一般方程分别为 的交线，则L与方程组（1)满足 z -O 1)L上的任意一点的坐标必 =0 满足方程组（1) 1z=0 2)满足方程组（1)的任意点 x=0 y=0 都在L上

二、空间直线的一般方程 1 : A1 x  B1 y C1 z  D1  0 2 : 2 2 2 2 A x B y C z D     0 设空间直线 L 为两平面 的交线，则 L 与方程组（1）满足 1 1 1 1 2 2 2 2 0 0 A x B y C z D A x B y C z D            （1） 1） L 上的任意一点的坐标必 满足方程组（1） 2）满足方程组（1）的任意点 称方程组（1）为直线 L 的一般方程 注记 2： x y z , , 轴的一般方程分别为 0 0 y z      0 0 x z      0 0 x y      都在 L 上

二、空间直线的一般方程 注记3：过直线 分析：投影直线既在平面Ⅱ上，也在过直线 Ax+By+Cz+D=0 L且与平面Π垂直的平面Π'上 42x+B2y+C2z+D2=0 解：过直线L且与Ⅱ垂直的平面'方程为 的平面方程为 1(x+y-2-1)+m(x-y+z+1)=0,(1) (4x+By+Cz+D)+ 即为(0+m)x+(0-my+(-1+m)z+(+m=0 +m(A2x+B2y+C22+D2)=0 由于平面'与平面Π垂直 其中实数1，m不同时为零 所以(l+m)1+(-m)1+(-l+m)-1=0. 例1求直线L: x+y-z-1=0 x-y+2+1=0 在平面 由此得1：m=1:(-1) 平面Π方程为2y-2z-2=0, :x+y+z=0上投影直线的方程 y-z-1=0 所以投影直线方程为 x+y+z=0

二、空间直线的一般方程 注记 3：过直线            0 0 2 2 2 2 1 1 1 1 A x B y C z D A x B y C z D 的平面方程为 l A x B y C z D  1 1 1 1          m A x B y C z D  2 2 2 2  0 其中 实数l m, 不同时为零. 例 1 求直线 1 0 : 1 0 x y z L x y z            在平面     : 0 x y z 上投影直线的方程 解：过直线 L 且与 垂直的平面方程为 l x y z m x y z ( 1) ( 1) 0, (1)         即为 ( ) ( ) ( ) ( ) 0 l m x l m y l m z l m           由于平面与平面 垂直 所以 ( ) 1 ( ) 1 ( ) 1 0. l m l m l m           由此得 l m: 1:( 1) .   平面方程为 2 2 2 0, y z    所以投影直线方程为 1 0 0 y z x y z          分析：投影直线既在平面 上，也在过直线 L 且与平面 垂直的平面上

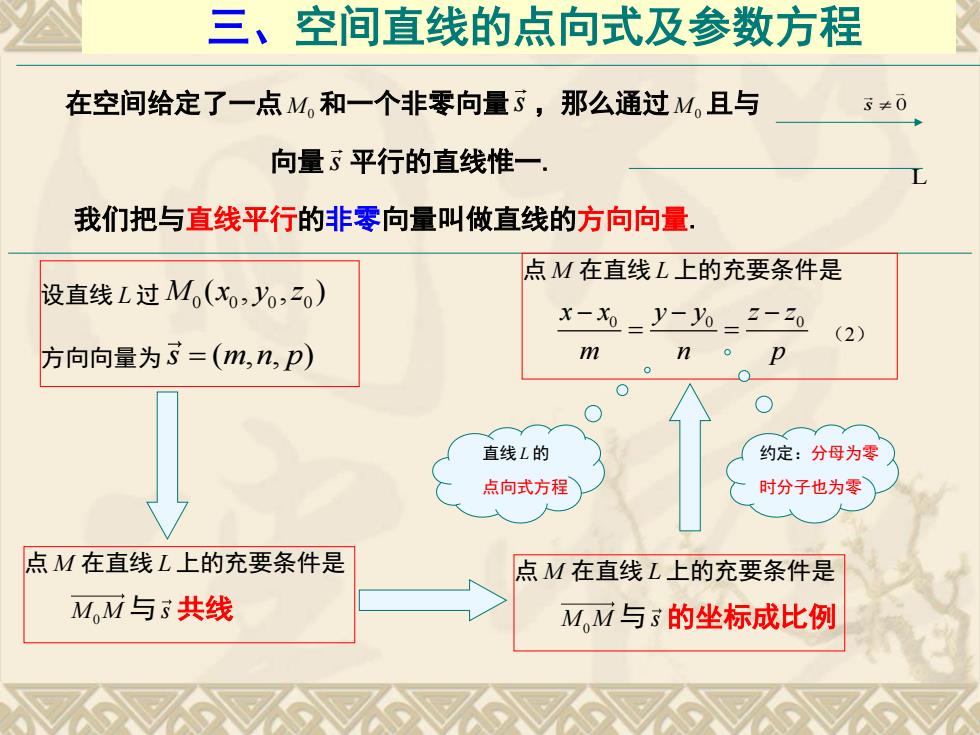
三、空间直线的点向式及参数方程 在空间给定了一点M,和一个非零向量了，那么通过M,且与 3≠0 向量平行的直线惟一 我们把与直线平行的非零向量叫做直线的方向向量. 点M在直线L上的充要条件是 设直线L过M(x,,20) x-x0=y-%=2-0 (2) 方向向量为S=(m,n,p) m n o D 直线L的 约定：分母为零 点向式方程 时分子也为零 点M在直线L上的充要条件是 点M在直线L上的充要条件是 MM与共线 MM与的坐标成比例

三、空间直线的点向式及参数方程 在空间给定了一点M0 和一个非零向量 s ，那么通过M0 且与 向量 s 平行的直线惟一. 我们把与直线平行的非零向量叫做直线的方向向量. s  0 L 我们称方程（2）为直线 L 的点向式方程 设直线 L 过 0 0 0 0 M x y z ( , , ) 方向向量为 s m n p  ( , , ) 点M 在直线 L 上的充要条件是 M M0 与s 共线 点M 在直线 L 上的充要条件是 M M0 与s 的坐标成比例 点 M 在直线 L 上的充要条件是 0 0 0 x x y y z z m n p      （2） 直线 L 的 点向式方程 约定：分母为零 时分子也为零