
§8.4多元复合函数的求导法则 主要 内容 中间变量为 中间变量为多 元函数 复合函数 元的函数 的求导法则 的求导法则 中间变量既 有一元函数 又有多元函 数的求导法则
中间变量为一 元函数 的求导法则 中间变量为多 元的函数 的求导法则 主 要 内 容 §8.4 多元复合函数的求导法则 复合函数 中间变量既 有一元函数 又有多元函 数的求导法则
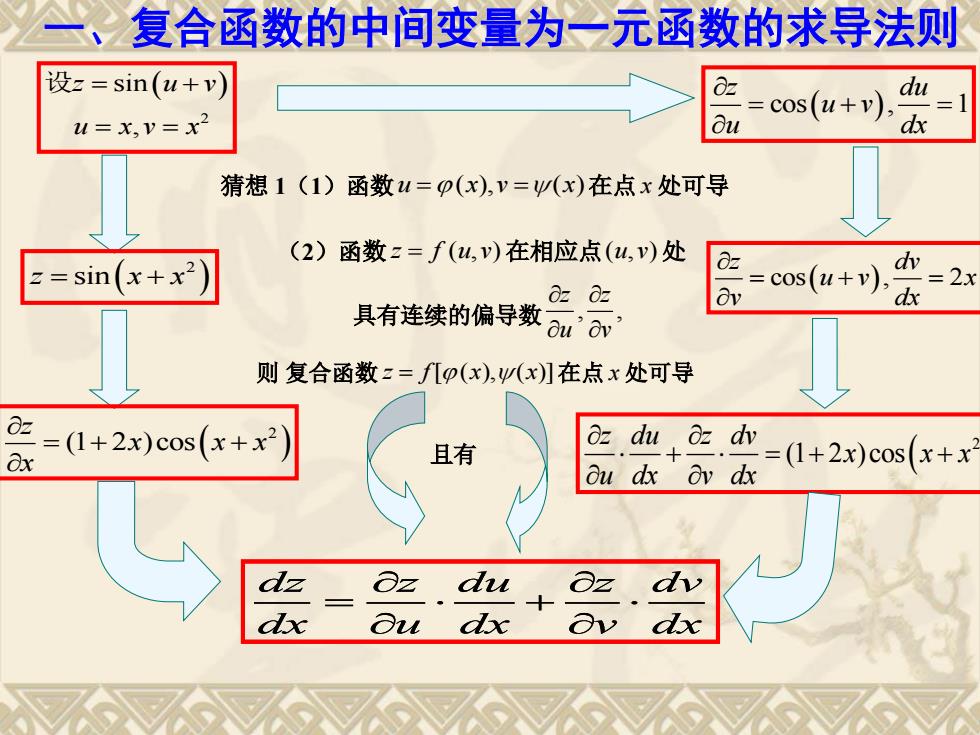
复合函数的中间变量为一元函数的求导法则 设z=sin(u+y cos(u+ du u=x,v=x2 猜想1(1)函数u=p(x),v=w(x)在点x处可导 (2)函数z=f(u,v)在相应点(u,v)处 z=sin(x+x2 cos(u+ = dv =2X 0z 0z 具有连续的偏导数 u'ov 则复合函数z=f几p(x),yW(x】在点x处可导 器-+2eas(r+ 且有 oz du oz dv ou dx ov dx =1+2x)c0s(x+x dz az du + Oz dv dx u dx av dx
一、复合函数的中间变量为一元函数的求导法则 2 sin , z u v u x v x 设 2 z x x sin 2 (1 2 )cos z x x x x cos , 1 z du u v u dx cos , 2 z dv u v x v dx 2 (1 2 )cos z du z dv x x x u dx v dx (2)函数 z f u v ( , ) 在相应点(u,v) 处 具有连续的偏导数 , , z z u v 则 复合函数 z f x x [ ( ), ( )] 在点 x 处可导 猜想 1(1)函数u (x),v (x)在点 x 处可导 且有 dz z du z dv dx u dx v dx dz z du z dv dx u dx v dx
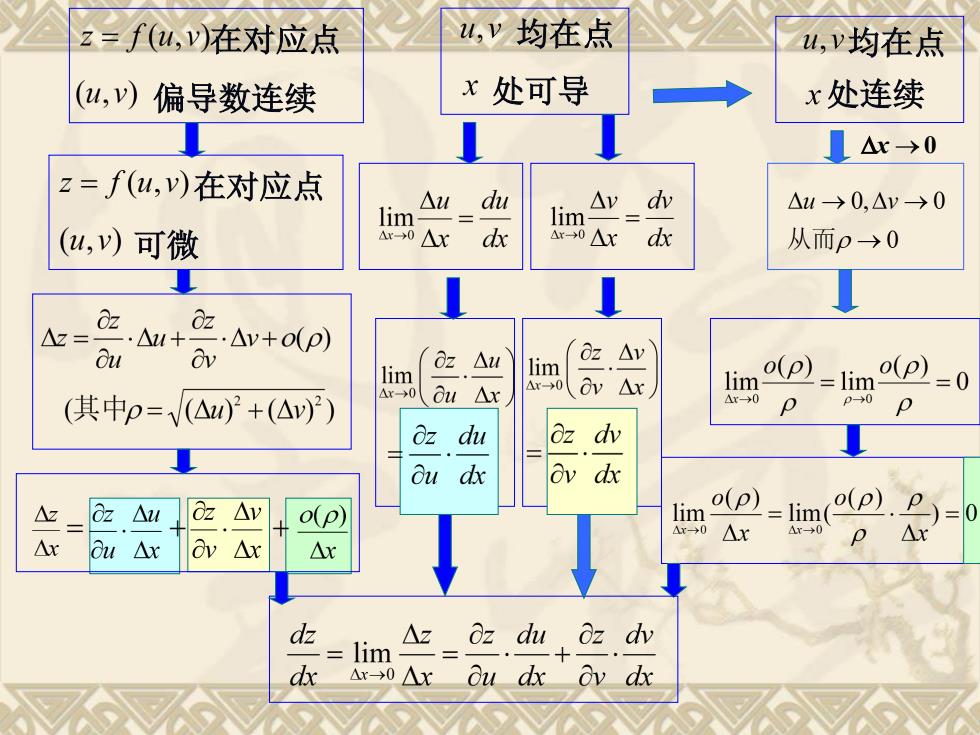
z=f(,v)在对应点 ,v均在点 山,P均在点 (u,)偏导数连续 x处可导 x处连续 △x→0 z=f(u,)在对应点 △udu △dw △u→0,△y→0 lim lim (u,)可微 Ar-0△x dx △r-0△xdx 从而p→0 O z.a+2.△v+o(p) 02 △z= o Ov z△u Oz△y lim lim lim o(p) =lim o(p) Ar>0 Ov△x =0 △x->0 (其中p=V(△)2+(△)2) ou△x △r0 P→0 Oz du oz dv Bu dx Ov dx △z 0z△u △v o(p) lim o(p)=lim( (p).P)=0 Ax0△x r→0 ou△x p△x △x △x △x dz =lim △z oz du,Oz dv △r→0△x Ou dx ov dx
均在点 处连续 在对应 点 偏导数连续 x 0 在对应 点 可微 均在点 处可导
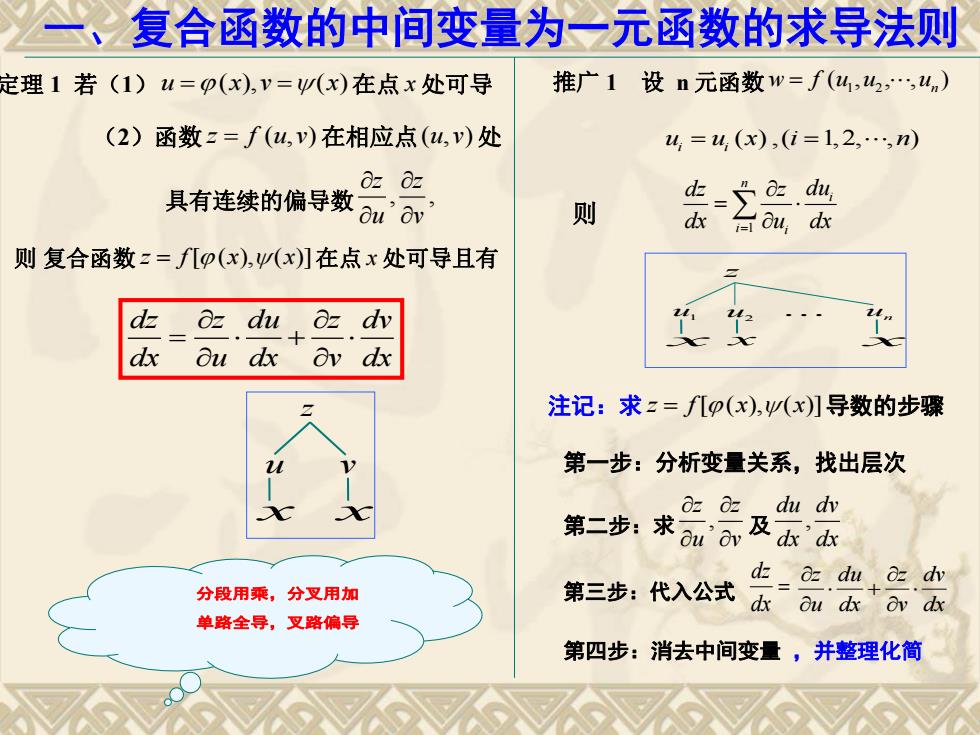
复合函数的中间变量为一元函数的求导法则 定理1若(1)u=p(x),v=W(x)在点x处可导 推广1设n元函数w=f(4,2,,n) (2)函数z=f(u,v)在相应点(u,v)处 4,=4(x),(i=1,2,…,n) 0z 0z 具有连续的偏导数 则 =.d dau,d 则复合函数z=fp(x),W(x】在点x处可导且有 Oz du oz dv dx au dx av dx 注记:求z=fLp(x),yW(x】导数的步骤 第一步:分析变量关系,找出层次 Oz B du dy 第二步:求及 do du o dv 分段用乘,分叉用加 第三步:代入公式kla 单路全导,叉路偏导 第四步:消去中间变量,并整理化简
一、复合函数的中间变量为一元函数的求导法则 (2)函数 z f u v ( , ) 在相应点(u,v) 处 具有连续的偏导数 , , z z u v 则 复合函数 z f x x [ ( ), ( )] 在点 x 处可导且有 定理 1 若(1)u (x),v (x)在点 x 处可导 dz z du z dv dx u dx v dx z u v x x 分段用乘,分叉用加 单路全导,叉路偏导 推广 1 设 n 元函数 ( , , , ) u1 u2 un w f ( ) ,( 1,2, , ) u u x i n i i 则 1 n i i i dz z du dx u dx u1 u2 z x x u n x 注记:求 z f[ (x),(x)]导数的步骤 第一步:分析变量关系,找出层次 第二步:求 , z z u v 及 , du dv dx dx 第三步:代入公式 dx dz dx dv v z dx du u z 第四步:消去中间变量 ,并整理化简
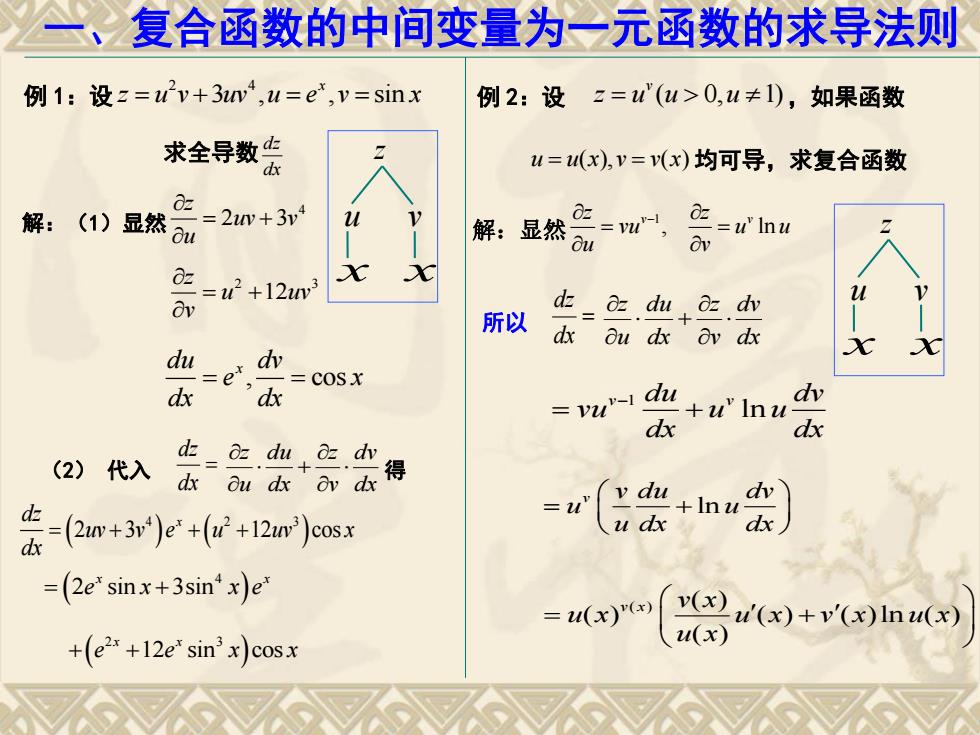
、复合函数的中间变量为一元函数的求导法则 例1:设z=u2v+3w,u=e,v=sinx 例2:设z='(u>0,u≠1),如果函数 求全导数 u=u(x),v=v(x)均可导,求复合函数 解: =2+3v (1)显然u 解:显然 =, =t'lnw O C2=+12w V d 所以 d=o.du odhy dx ou dx Ov dx du dx dx =COSx vu"-1 du +u'Inu dv dx dx (2)代入 会在气我得 =u" v du dv 东-r+n)p++1m)sx u dx dx =(2e'sinx+3sin'x)e =2u(x)() ()+v()() +(e+12e'sin'x)cosx u(x)
一、复合函数的中间变量为一元函数的求导法则 例 1:设 2 4 3 , , sin x z u v uv u e v x 求全导数 dz dx z u v x x 解:(1)显然 4 2 3 z uv v u 2 3 12 z u uv v , cos du dv x e x dx dx (2) 代入 dx dz dx dv v z dx du u z 得 4 2 3 2 3 12 cos dz x uv v e u uv x dx 4 2 sin 3sin x x e x x e 2 3 12 sin cos x x e e x x 例 2:设 ( 0, 1) v z u u u ,如果函数 u u x v v x ( ), ( ) 均可导,求复合函数 z u v x x 解:显然 1 , ln z z v v vu u u u v 所以 dx dz dx dv v z dx du u z 1 ln v v du dv vu u u dx dx ln v v du dv u u u dx dx ( ) ( ) ( ) ( ) ( )ln ( ) ( ) v x v x u x u x v x u x u x