南阳师范学院：《高等数学》课程教学资源（课件讲稿）第八章 多元函数微分法及其应用 第六节 多元函数微分法的几何应用举例

§8.6多元函数微分法的几何应用举例 空间曲面的切 平 面与法线 空间曲线的切 曲线的参数方 线 主要 内容 程 与法平面 及一般方程 曲面隐函数方 程及 显函数方程

空间曲线的切 线 与法平面 §8.6 多元函数微分法的几何应用举例 曲线的参数方 程 及一般方程 空间曲面的切 平 面与法线 主要 内容 曲面隐函数方 程及 显函数方程

空间曲线的切线与法平面 过空间曲线r两点M与M',作割线MM'当点M'沿曲线T趋于点M时， 如果割线MM'趋于极限位置MT,那么直线MT就称为曲线T在点M处的切线 M' M M x=p(t) 如何求空间曲线「 y=w(t) 如何求空间曲线厂 E(x,y,z）=0 2=o(t) E(x,y,z)=0 上过点 上过点M(xo,yo,2o) M(xo,0)的切线方程？ 的切线方程？

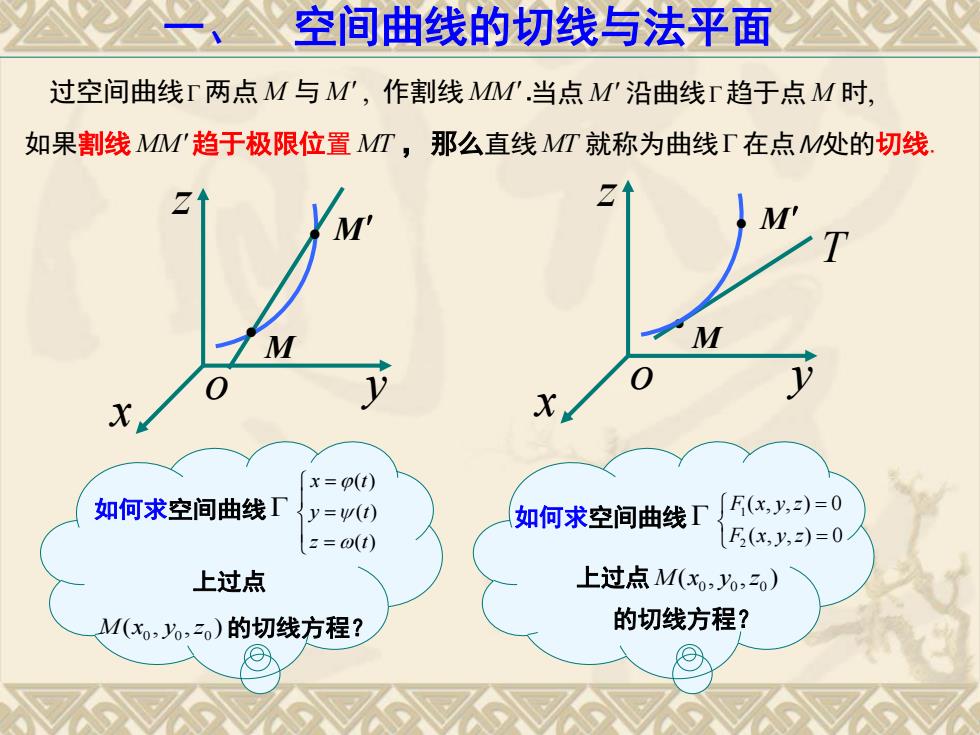
过空间曲线两点M 与M  作割线MM.当点M 沿曲线趋于点M 时 如果割线MM趋于极限位置MT ，那么直线MT 就称为曲线 在点Ｍ处的切线. o z y x M   M M  o z y x  M T 一、 空间曲线的切线与法平面 如何求空间曲线 1 2 ( , , ) 0 ( , , ) 0 F x y z F x y z      上过点 0 0 0 M x y z ( , , ) 的切线方程？ 如何求空间曲线 ( ) ( ) ( ) x t y t z t            上过点 0 0 0 M x y z ( , , )的切线方程？

空间曲线的切线与法平面 探究：在T上取对应于t=t。+△t时的点为 设x=p(t),y=yw(),2=0(t)在。处可导 M(x+△x,y%+△y,20+△x) 且p'(t),w(t),o'(t)不同时为零 曲线的割线MM'的方程为 当M'→M时，△t→0割线MM'趋于极限位置 x-0=y-6=2-0 Ar △y MT就是曲线Γ在点M的切线. 取极限 切线方程 曲线的割线MM'的方程为 2-30 X-龙=y-%=3-0 x-0-y-6= △x △y (t)w'(to) @'(t) △t △t △t

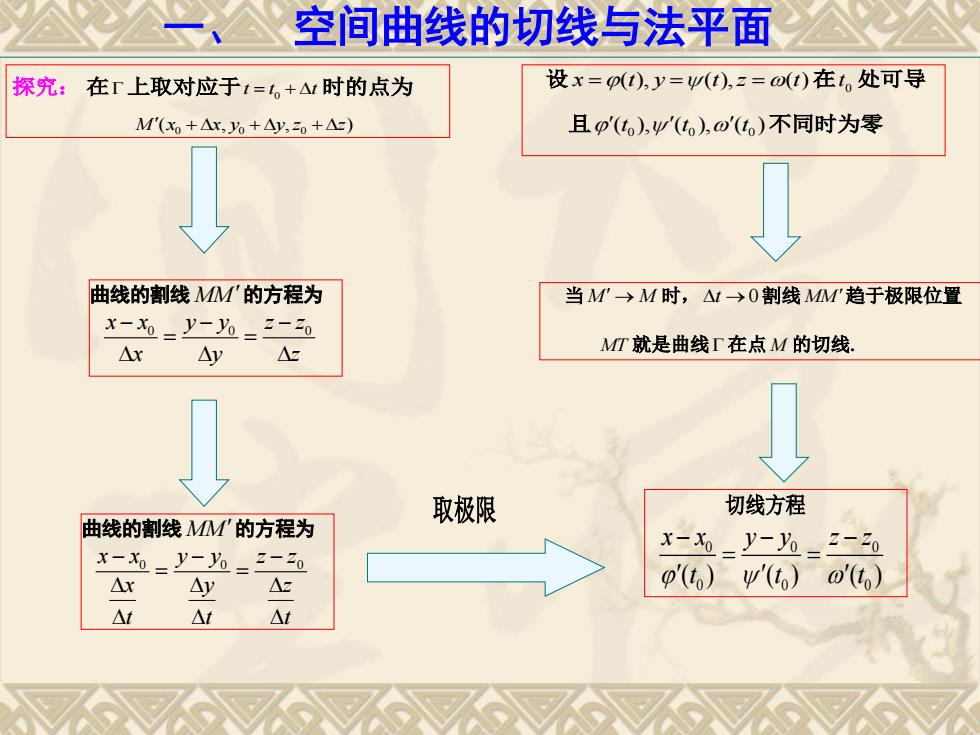
一、 空间曲线的切线与法平面 探究： 在上取对应于 0 t t t    时的点为 0 0 0 M x x y y z z ( , , )       曲线的割线 MM的方程为 0 0 0 x x y y z z xyz       曲线的割线 MM的方程为 0 0 0 x x y y z z xyz t t t          当 M M   时， t 0割线MM趋于极限位置 MT 就是曲线 在点M 的切线. 设 x t y t z t       ( ), ( ), ( )在 0 t 处可导 且 0 0 0       ( ), ( ), ( ) t t t 不同时为零 取极限 切线方程 0 0 0 0 0 0 ( ) ( ) ( ) x x y y z z    t t t      

空间曲线的切线与法平面 定理1(1)x=0(),y=w(),z=0(t)在t。处可导 过切点与切线垂直的平面称 为曲线的法平面 且0'()，yw(t),o'()不同时为零 x=o(t) 注记1（1)y=w(x),z=o(x)在x,处可导 (2)空间曲线r: {y=w)对应于t=。 且W(x),o(x)不同时为零 (z=0(t) 时的点M(xo,o) (2)曲线r: y=v(x) 2=o)上一点M(6) 则（1)曲线r过点M的切线方程为 则(1)曲线r过点M的切线方程为 x-0=y-%=-0 '(to)w'(to)'(to) x-龙=y-=2-0 1w'(x)'(x) (2)曲线r过点M法平面方程为 (2)曲线r过点M法平面方程为 p'(t)x-x)+w(t)y-)+o'(t)(z-2)=0 (x-x)+W'(x)(y-y)+o'(x)(z-z)=0

一、 空间曲线的切线与法平面 定理 1（1） x t y t z t       ( ), ( ), ( )在 0 t 处可导 且 0 0 0       ( ), ( ), ( ) t t t 不同时为零 （2）空间曲线： ( ) ( ) ( ) x t y t z t            对应于 0 t t  时的点 0 0 0 M x y z ( , , ) 则（1）曲线过点M 的切线方程为 0 0 0 0 0 0 ( ) ( ) ( ) x x y y z z    t t t       （2）曲线过点M 法平面方程为 0 0 0 0 0 0       ( )( ) ( )( ) ( )( ) 0 t x x t y y t z z       过切点与切线垂直的平面称 为曲线的法平面 注记 1（1） y x z x     ( ), ( )在 0 x 处可导 且 0 0     ( ), ( ) x x 不同时为零 （2）曲线： ( ) ( ) y x z x        上一点 0 0 0 M x y z ( , , ) 则（1）曲线过点M 的切线方程为 0 0 0 0 0 1 ( ) ( ) x x y y z z   x x        （2）曲线过点M 法平面方程为 0 0 0 0 0 ( ) ( )( ) ( )( ) 0 x x x y y x z z          

空间曲线的切线与法平面 注记2：求空间曲线切线方程及法面方程步骤 x=1 例1：求空间曲线「： y=2在点M(1,1,1) xo=(to) z=p (1)确定M(x,,20): =w() 的切线方程及法平面方程 20=0(t6) 解：显然当空间曲线Γ过点M(1,1,1)时t。=1 (2)确定切线的方向向量 又 x'=1,y'=2t,z=3t2 s=(p'(t),w'(t),o'(to) 所以 x6==1y61=2,26=3 (3)写出切线的标准方程 因此切线的方向向量3=(1,2,3) x-0=y-%=2-0 x-1-y-1_2-1 '(to)v'(to)'(to) 故切线方程 1 23 (4)写出法平面的法式方程 法平面的法式方程 1(x-1)+2.(y-1)+3.(z-1)=0 p'(t)x-x)+w'()y-)+0'(t)(z-2o)=0 即 x+2y+3z-6=0=0

一、 空间曲线的切线与法平面 注记 2：求空间曲线切线方程及法面方程步骤 （1）确定 0 0 0 M x y z ( , , ): 0 0 0 0 0 0 ( ) ( ) ( ) x t y t z t            （2）确定切线的方向向量 s t t t        ( ), ( ), ( ) 0 0 0  （3）写出切线的标准方程 0 0 0 0 0 0 ( ) ( ) ( ) x x y y z z    t t t       （4）写出法平面的法式方程 0 0 0 0 0 0       ( )( ) ( )( ) ( )( ) 0 t x x t y y t z z       例 1：求空间曲线 : 2 3 x t y t z t         在点 M(1,1,1) 的切线方程及法平面方程 解：显然当空间曲线 过点 M(1,1,1)时 0 t 1 又 2 x y t z t      1, 2 , 3 所以 0 0 0 x y z   t t t    1 1 1    1, 2, 3 因此切线的方向向量 s  1,2,3 故切线方程 1 1 1 1 2 3 x y z      法平面的法式方程 1 ( 1) 2 ( 1) 3 ( 1) 0          x y z 即 x y z      2 3 6 0 0