第六章△微分方程 可分离 变量 二阶微 基本 一阶微 分方程 概念 分方程 高阶微 分方程
可分离 变量 二阶微 分方程 一阶微 分方程 高阶微 分方程 基 本 概 念 第六章 微分方程
6.1微分万程的基本慨念 主要 内容 概念产 微分方 生的背景 程的定义 微分方 程的解
主 要 内 容 微分方 程的解 概念产 生的背景 微分方 程的定义 §6.1 微分方程的基本概念
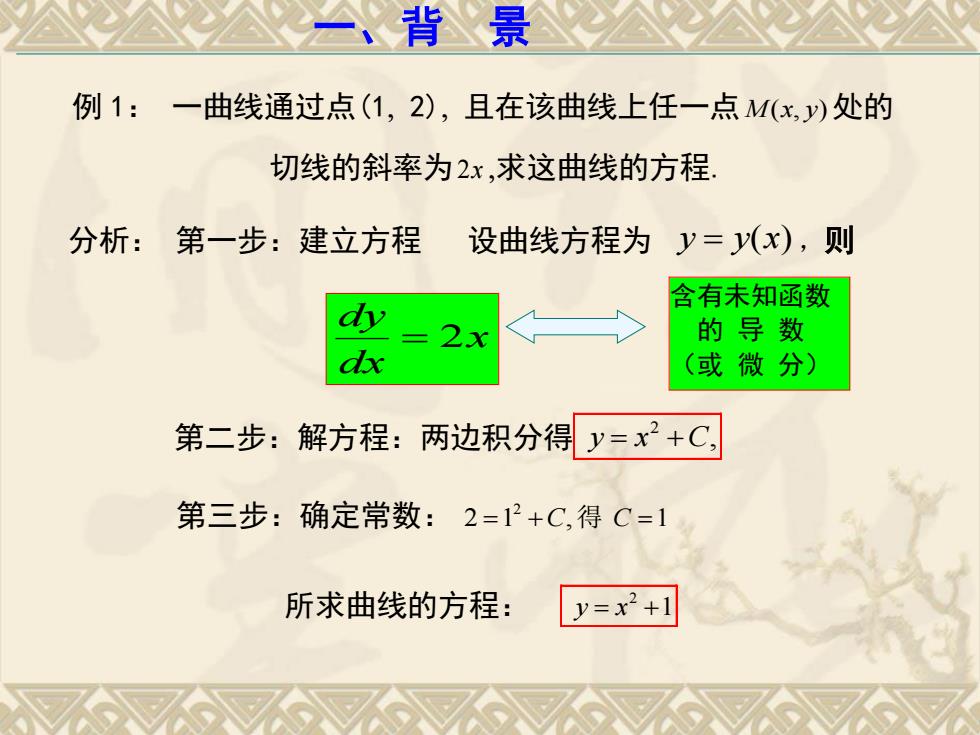
背景 例1:一曲线通过点(1,2),且在该曲线上任一点M(x,y)处的 切线的斜率为2x,求这曲线的方程 分析:第一步:建立方程 设曲线方程为 y=y(x),则 含有未知函数 的导数 (或微分) 第二步:解方程:两边积分得y=x2+C, 第三步:确定常数:2=12+C,得C=1 所求曲线的方程: y=x2+1
一、背 景 例 1: 一曲线通过点(1 2) 且在该曲线上任一点M x y ( , )处的 切线的斜率为2x 求这曲线的方程. 分析: 第一步:建立方程 设曲线方程为 y y(x) ,则 x dx dy 2 第二步:解方程:两边积分得 , 2 y x C 第三步:确定常数: 2 1 , 2 C 得 C 1 所求曲线的方程: 1 2 y x 含有未知函数 的 导 数 (或 微 分)

二、微分方程的定义 定义1:含有未知函数导数(或微分)的方程叫微分方程 未知函数是一元的微分的方程叫做常微分方程 未知函数是多元的微分的方程叫做偏微分方程 微分方程中所出现的未知函数的最高阶导数的阶数,叫微分方程的阶 一般n阶微分方程: F(x.y.y..y)=0 或 ym=fx,y,y',…,ym-) 注记1:在微分方程中,自变量和未知函数可以不出现, 但未知函数的导数或微分必须出现
定义 1:含有未知函数导数(或微分)的方程叫微分方程 未知函数是一元的微分的方程叫做常微分方程 未知函数是多元的微分的方程叫做偏微分方程 微分方程中所出现的未知函数的最高阶导数的阶数 叫微分方程的阶 一般n阶微分方程 二、微分方程的定义 ( ) ( , , , , ) 0 n F x y y y 或 ( ) ( 1) ( , , , , ) n n y f x y y y 注记 1:在微分方程中,自变量和未知函数可以不出现, 但未知函数的导数或微分必须出现

微分方程的定义 课堂训练1: 下列不是微分方程的是() A: dy dx =2Xy B:(7x-6y)k+(x+y)dy=0 C: D:x=-28r2+W1+ E:y'+y=0 F:y"+2y'+y-2x=0
二、微分方程的定义 课堂训练 1: 下列不是微分方程的是( ) xy dx dy A: 2 B:(7x 6y)dx (x y)dy 0 g dt d x C 2 2 : 0 0 2 2 1 D : x gt v t x E : y y 0 F : y 2y y 2x 0