第九章重积分及曲线积分 二重积分及应用 主要内容 三重积分及应用 曲线积分 曲面积分
二重积分及应用 三重积分及应用 曲线积分 主 要 内 容 曲面积分 第九章 重积分及曲线积分
§9.1二重积分的概念及性质 概念产生的背景 二重积分的概念 主要内容 二重积分的性质 二重积分性质的应用
概念产生的背景 二重积分的概念 二重积分的性质 二重积分性质的应用 主 要 内 容 §9.1 二重积分的概念及性质
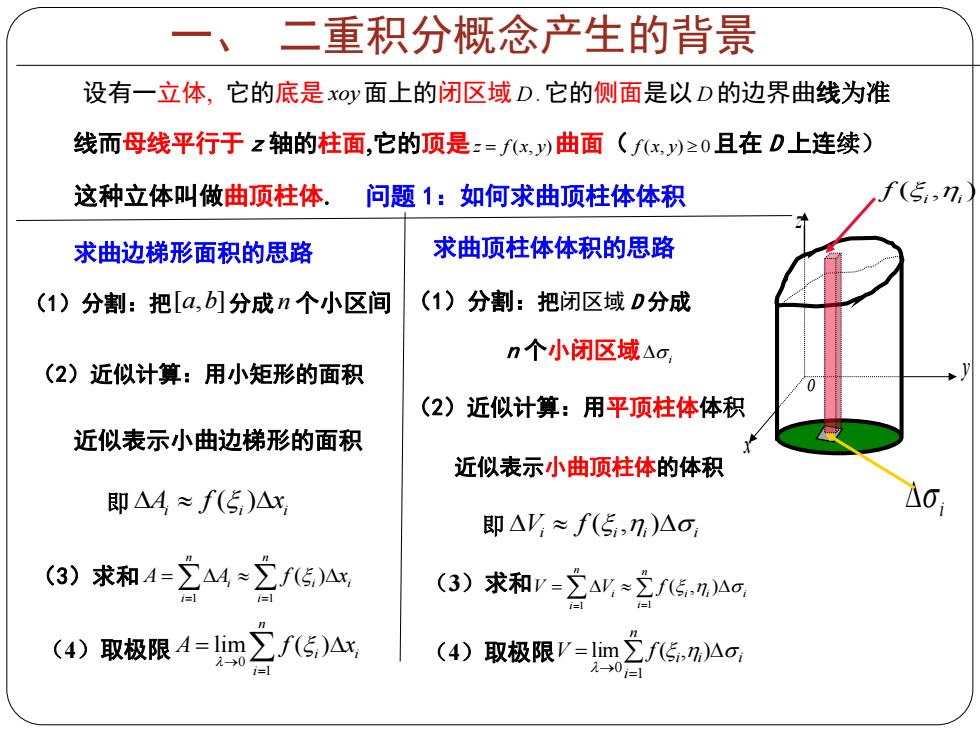
一、二重积分概念产生的背景 设有一立体,它的底是x0y面上的闭区域D.它的侧面是以D的边界曲线为准 线而母线平行于z轴的柱面,它的顶是:=fx,)曲面(fx,)≥0且在D上连续) 这种立体叫做曲顶柱体。问题1:如何求曲顶柱体体积 (5,7,》 求曲边梯形面积的思路 求曲顶柱体体积的思路 (1)分割:把[a,b]分成n个小区间 (1)分割:把闭区域D分成 n个小闭区域△a (2)近似计算:用小矩形的面积 (2)近似计算:用平顶柱体体积 近似表示小曲边梯形的面积 近似表示小曲顶柱体的体积 即A4≈f(5)△x 即△V,≈f(5,7)△ (3) 求和A=2AM∑f5)Ax (3)求和r-2a业2.na (4) 取极限A=lim∑f传)△x (4) 元0 取极限V=m2f传△a, 201
设有一立体 它的底是 xoy面上的闭区域D .它的侧面是以D的边界曲线为准 线而母线平行于 z 轴的柱面它的顶是z f x y ( , )曲面( f x y ( , ) 0 且在 D 上连续) 这种立体叫做曲顶柱体 x z y o D 问题 1:如何求曲顶柱体体积 求曲边梯形面积的思路 (1)分割:把[ , ] a b 分成 n 个小区间 (2)近似计算:用小矩形的面积 近似表示小曲边梯形的面积 即 ( ) A f x i i i (3)求和 1 1 ( ) n n i i i i i A A f x (4)取极限 0 1 lim ( ) n i i i A f x (1)分割:把闭区域 D 分成 n 个小闭区域 i (2)近似计算:用平顶柱体体积 近似表示小曲顶柱体的体积 即 ( , ) V f i i i i (3)求和 1 1 ( , ) n n i i i i i i V V f 求曲顶柱体体积的思路 i ( , ) i i f (4)取极限 i i i n i V f lim ( , ) 1 0 一、 二重积分概念产生的背景
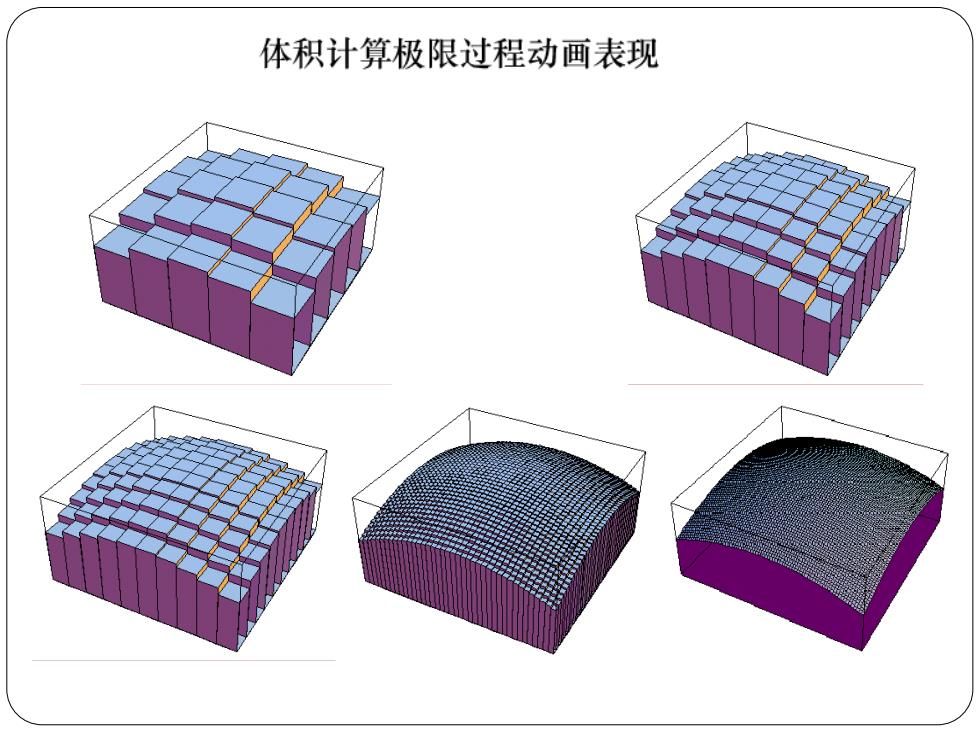
体积计算极限过程动画表现

二、二重积分的概念 1.二重积分的定义 设fx,y)是有界闭区域D上的有界函数. (1)将闭区域D任意分成n个小闭区域△o,△o2,,△on其中△o,表示第i个小区域 也表示它的面积. (2)在每个Ag,上任取-点(5,),作乘积f,n)△a,并作和2/怎,)Aa. I- (3)如果当无限增大且各小闭区域的直径中的最大值入趋于零时,这和的极限总存在 则称此极限为函数f(x,y)在闭区域D上的二重积分,记作∬xo,即 D 即 f(x.yxlo-lim2f(m)Aa, D →01 D f(x,y) x,y f(x,y)do do f(.)Ac, 1=1 积分区域 被积函数 积分变量 被积表达式 面积元素 积分和
1. 二重积分的定义 设 f x y ( , )是有界闭区域 D 上的有界函数 (1)将闭区域 D 任意分成 n 个小闭区域 1 2, n 其中 i表示第 i 个小区域 也表示它的面积 (2)在每个 i上任取一点( i i) 作乘积 ( , ) , i i i f 并作和 i i i n i f ( , ) 1 (3)如果当n 无限增大且各小闭区域的直径中的最大值 趋于零时 这和的极限总存在 则称此极限为函数 f x y ( , )在闭区域 D 上的二重积分 记作 f x y d D ( , ) 即 即 i i i n D i f x y d f ( , ) lim ( , ) 1 0 D 积分区域 f x y ( , ) 被积函数 x y, 积分变量 f x y d ( , ) 被积表达式 d 面积元素 1 ( , ) n i i i i f 积分和 二、 二重积分的概念