§8.7多元函数的极值及算法 多元函数极值 的应用 多元函数的极 主要 多元函数的条 值 内容 件极值 多元函数的 最值
§8.7 多元函数的极值及算法 多元函数的极 值 多元函数的条 件极值 多元函数极值 的应用 多元函数的 最值 主要 内容
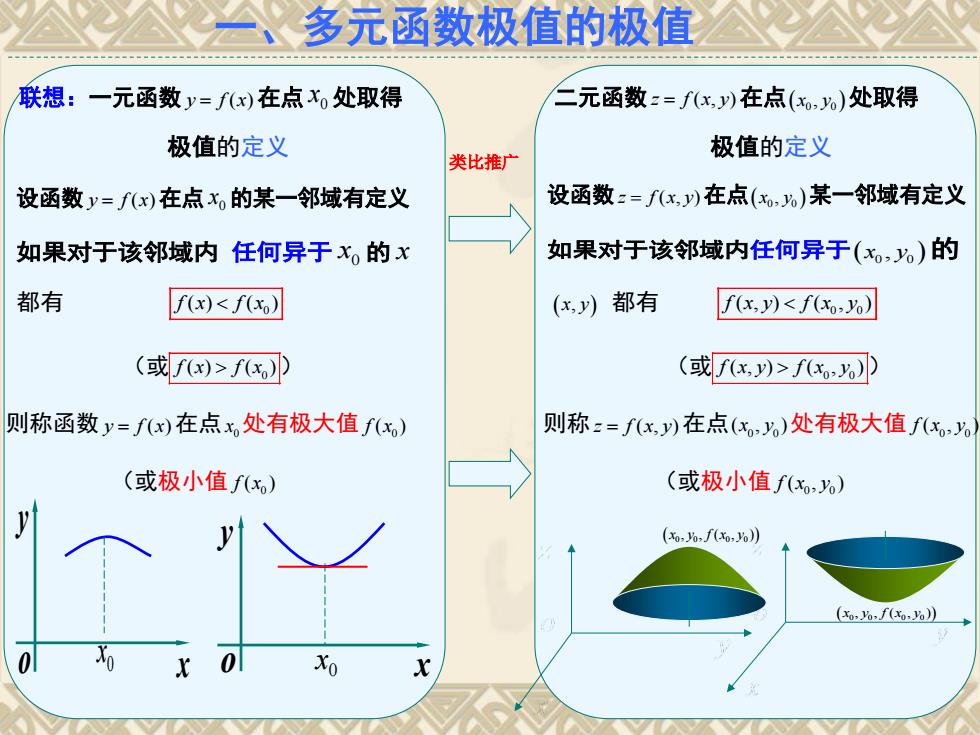
多元函数极值的极值 联想:一元函数y=fx)在点x处取得 二元函数:=fx,)在点(x,)处取得 极值的定义 类比推广 极值的定义 设函数y=fx)在点x的某一邻域有定义 设函数:=fx,y)在点(x,)某一邻域有定义 如果对于该邻域内任何异于x,的x 如果对于该邻域内任何异于(x。)的 都有 f(x)<f(xo) (x,y)都有 f(x,y)<f(xo-Yo) (或fx)>fx)) (或fx)>fx) 则称函数y=fx)在点x,处有极大值f(x) 则称:=fx,y)在点(x,)处有极大值fx (或极小值fx) (或极小值fx) y (x0,6,f(,6) (xo,%,f(,%)) 0 0 Xo
一、多元函数极值的极值 联想:一元函数 y f x ( )在点 0 x 处取得 极值的定义 类比推广 设函数 y f x ( )在点 0 x 的某一邻域有定义 如果对于该邻域内 任何异于 0 x 的 x 都有 0 f x f x ( ) ( ) (或 0 f x f x ( ) ( ) ) 则称函数 y f x ( )在点 0 x 处有极大值 0 f x( ) (或极小值 0 f x( ) x y o 0 x x y o 0 x 二元函数z f x y ( , )在点 x y 0 0 , 处取得 极值的定义 设函数z f x y ( , )在点 x y 0 0 , 某一邻域有定义 如果对于该邻域内任何异于 x y 0 0 , 的 x y, 都有 0 0 f x y f x y ( , ) ( , ) (或 0 0 f x y f x y ( , ) ( , ) ) 则称 z f x y ( , )在点 0 0 ( , ) x y 处有极大值 0 0 f x y ( , ) (或极小值 0 0 f x y ( , ) x y f x y 0 0 0 0 , , ( , ) x y f x y 0 0 0 0 , , ( , )
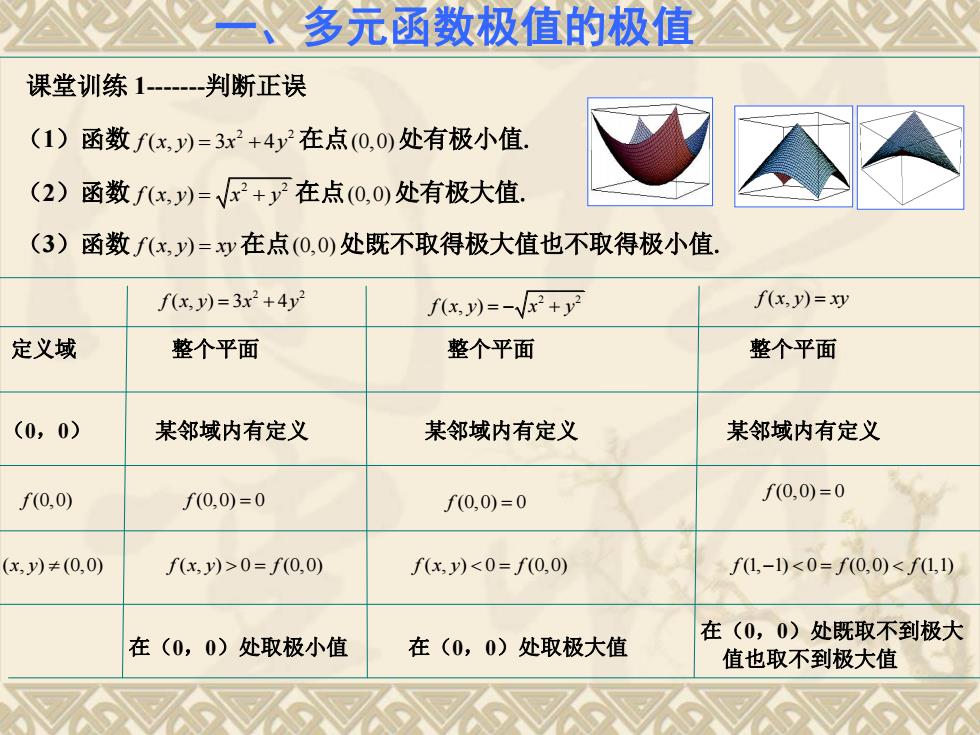
多元函数极值的极值 课堂训练1--判断正误 (1)函数fx,)=3x2+4y2在点(0,0)处有极小值. (2)函数fx,y)=√x2+y在点(0,0)处有极大值, (3)函数fx,)=y在点(0,0)处既不取得极大值也不取得极小值. fx,y)=3x2+4y2 fx,)=-√2+y f(x,y)=xy 定义域 整个平面 整个平面 整个平面 (0,0) 某邻域内有定义 某邻域内有定义 某邻域内有定义 f(0,0) f(0,0)=0 f(0,0)=0 f(0,0)=0 (x,y)≠(0,0) f(x,y)>0=f0,0) f(x,y)<0=f(0,0) fL1,-1)<0=f0,0)<f1,1) 在(0,0)处既取不到极大 在(0,0)处取极小值 在(0,0)处取极大值 值也取不到极大值
课堂训练 1-------判断正误 (1)函数 2 2 f x y x y ( , ) 3 4 在点(0,0)处有极小值 (2)函数 2 2 f x y x y ( , ) 在点(0,0)处有极大值 (3)函数 f x y xy ( , ) 在点(0,0)处既不取得极大值也不取得极小值 2 2 f x y x y ( , ) 3 4 2 2 f x y x y ( , ) f x y xy ( , ) 定义域 整个平面 整个平面 整个平面 (0,0) 某邻域内有定义 某邻域内有定义 某邻域内有定义 f (0,0) 0 f (0,0) 0 f (0,0) 0 ( , ) (0,0) x y f x y f ( , ) 0 (0,0) f x y f ( , ) 0 (0,0) f f f (1, 1) 0 (0,0) (1,1) 在(0,0)处取极小值 在(0,0)处取极大值 在(0,0)处既取不到极大 值也取不到极大值 f (0,0) 一、多元函数极值的极值

多元函数极值的极值 联想:一元函数y=f(x)在点Xo 类比猜测 二元函数:=f(x,y)在点(x%) 处取得极值的必有条件 处取得极值的必有条件 定理1 设函数y=f(x)在点x可导 设函数:=∫x,)在点(x) 若该函数在x,处取得极值 类比清测 有偏导数,若对该函数在 则必有 (,%)取得极值,则必有 f(x)=0 f(6)=0,f(x6)=0 满足该方程的点称为驻点 满足该方程的点称为驻点
一、多元函数极值的极值 联想:一元函数 y f x ( ) 在点 0 x 处取得极值的必有条件 设函数 y f x ( )在点 0 x 可导 若该函数在 0 x 处取得极值 则必有 0 f x ( ) 0 满足该方程的点称为驻点 二元函数 z f x y ( , )在点 x y 0 0 , 处取得极值的必有条件 类比猜测 设函数z f x y ( , )在点 x y 0 0 , 有偏导数,若对该函数在 x y 0 0 , 取得极值,则必有 0 0 0 0 ( , ) 0, ( , ) 0 x y f x y f x y 满足该方程的点称为驻点 类比猜测 定理 1
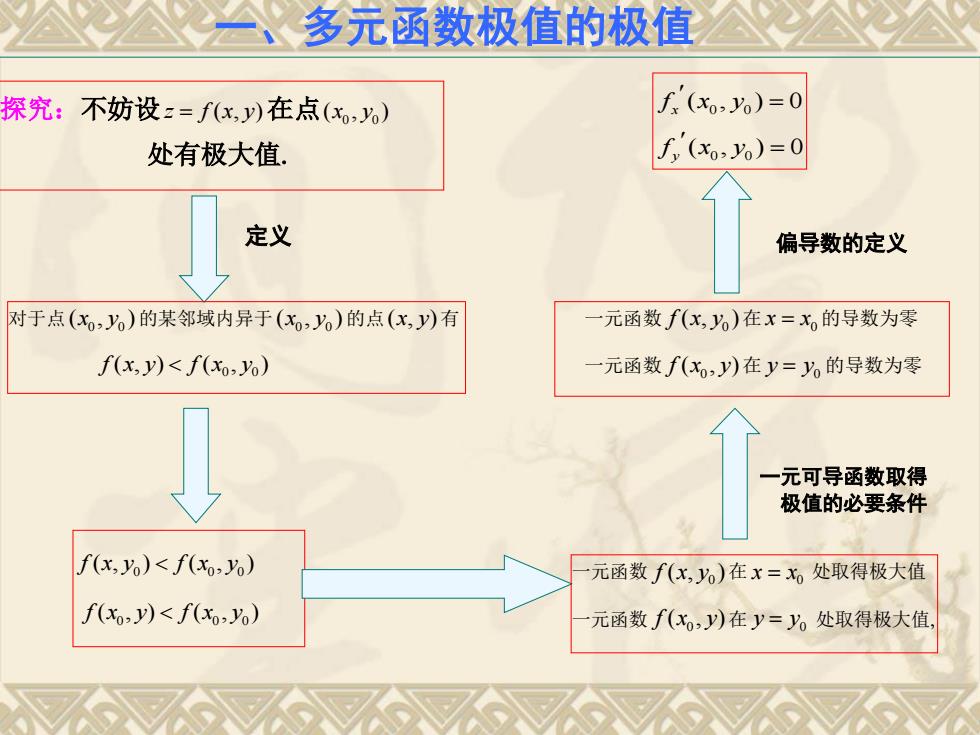
多元函数极值的极值 探究:不妨设z=f(x,y)在点(x) f (xo2 o)=0 处有极大值. f(xo,)=0 定义 偏导数的定义 对于点(x,y)的某邻域内异于(x,0)的点(x,y)有 元函数f(x,y)在x=x的导数为零 f(x,y)<f(x,%) 元函数f(x,y)在y=y的导数为零 元可导函数取得 极值的必要条件 f(x,Yo)<f(Xo>Yo) 元函数f(x,y)在x=x处取得极大值 f(Xo-y)<f(xo>Yo) 元函数f(xo,y)在y=y。处取得极大值
探究:不妨设z f x y ( , )在点 0 0 ( , ) x y 处有极大值 对于点 0 0 ( , ) x y 的某邻域内异于 0 0 ( , ) x y 的点 ( , ) x y 有 0 0 f x y f x y ( , ) ( , ) 0 0 0 f x y f x y ( , ) ( , ) 0 0 0 f x y f x y ( , ) ( , ) 定义 一元函数 0 f x y ( , )在 0 x x 处取得极大值 一元函数 0 f x y ( , )在 0 y y 处取得极大值 一元函数 0 f x y ( , )在 0 x x 的导数为零 一元函数 0 f x y ( , )在 0 y y 的导数为零 一元可导函数取得 极值的必要条件 偏导数的定义 0 0 0 0 ( , ) 0 ( , ) 0 x y f x y f x y 一、多元函数极值的极值