第一节映射与函数 例3设f: →1,小.对每个x引 f=smx,则/是一个映射,定义域D,引 值域Rr=[-1,1]. 1 元 2 f(x)=sin x 元 2 上页 下页 返回 MathGS 公式 线与面 数学家
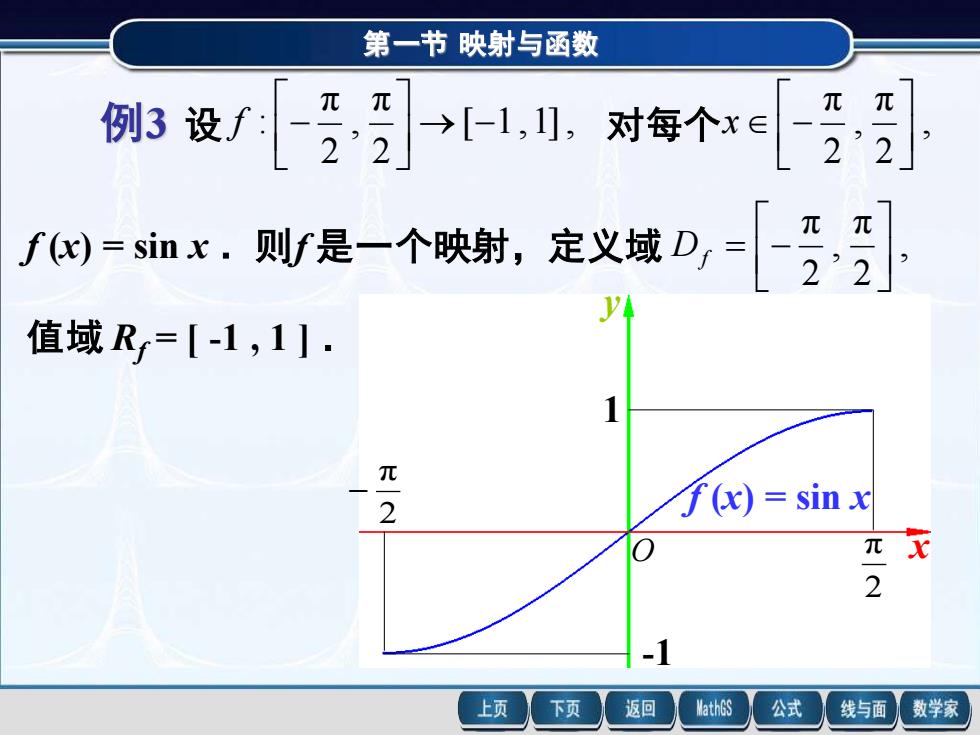
第一节 映射与函数 例3 设 f (x) = sin x .则f 是一个映射,定义域 值域 Rf = [ -1 , 1 ] . [ 1,1], 2 π , 2 π : → − f − 对每个 , 2 π , 2 π x − , 2 π , 2 π Df = − x y f (x) = sin x -1 1 2 π − 2 O π

第一节映射与函数 对映射f:X→Y 若f(X)=Y,则称f为满射 X 满射 上面的例2是满射. 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 映射与函数 对映射 若 f (X ) = Y , 则称 f 为满射. X Y f 满射 上面的 是满射.第一节 映射与函数 例2 设 X = {(x , y) | x 2 + y 2 = 1},Y = {(x , 0) | x 1 }, 与之对应. f : X→Y,则对每个 (x , y) X,有唯一确定的(x , 0) Y 显然f 是一个映射,定义域 Df = X ,值域 Rf = Y .在几何上,这个映射表示将平面上一个圆心在 原点的单位圆上的点投影到 x 轴上的区间 [ -1 , 1 ]上. 1 1 (x , y) x (x , -y) x y -1 -1 O
第一节映射与函数 对映射f:X→Y 若:1,2∈X,x1≠x2,有 f()≠f(x2) 则称f为单射 X 单射 上面的例3是单射. 上页 下页 返回 MathGS 公式 线与面 数学家
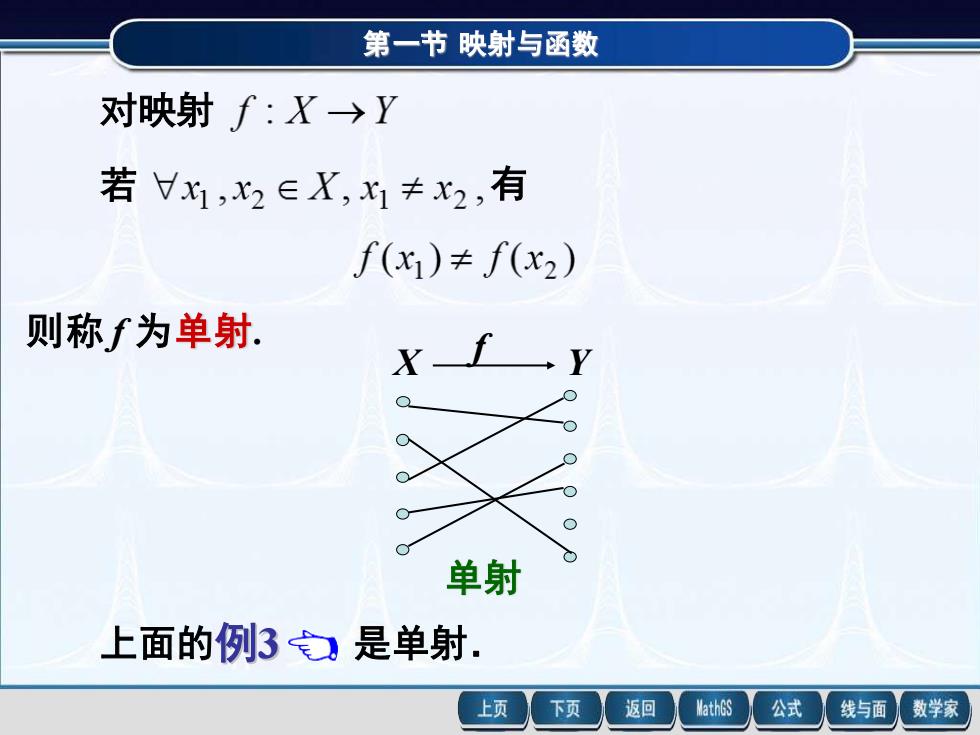
第一节 映射与函数 若 有 则称 f 为单射. 对映射 X Y f 单射 上面的 是单射. 第一节 映射与函数 例3 设 f (x) = sin x .则f 是一个映射,定义域 值域 Rf = [ -1 , 1 ] . [ 1,1], 2 π , 2 π : → − f − 对每个 , 2 π , 2 π x − , 2 π , 2 π Df = − x y f (x) = sin x -1 1 2 π − 2 O π
第一节映射与函数 对映射f:X→Y 若f既是满射又是单射,则称f为双射或一一映射. X 双射 上面的例3既是单射又是满射,故是双射. 上页 下页 返回 MathGS 公式 线与面 数学家
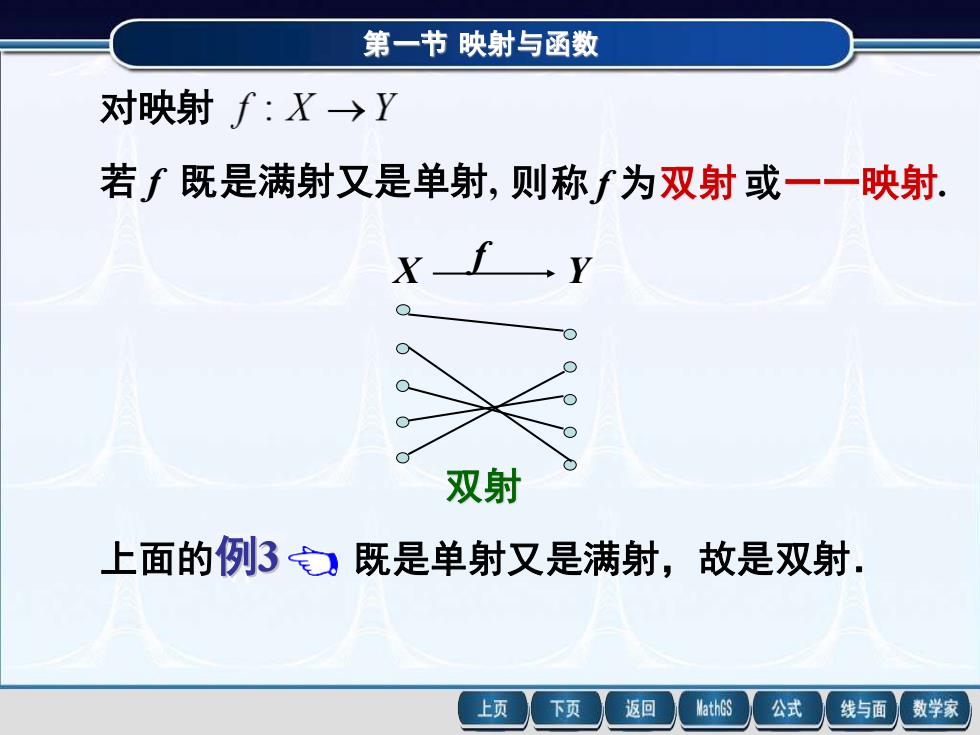
第一节 映射与函数 若 f 既是满射又是单射, 则称 f 为双射 或一一映射. 对映射 X Y f 双射 上面的 既是单射又是满射,故是双射. 第一节 映射与函数 例3 设 f (x) = sin x .则f 是一个映射,定义域 值域 Rf = [ -1 , 1 ] . [ 1,1], 2 π , 2 π : → − f − 对每个 , 2 π , 2 π x − , 2 π , 2 π Df = − x y f (x) = sin x -1 1 2 π − 2 O π

第一节映射与函数 说明 映射又称为算子.在不同数学分支中有不同的惯用 名称.例如, X(丰☑) 一Y(数集) f称为X上的泛函 X(丰) f称为X上的变换 X(数集或点集) 一R f称为定义在X上的函数 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 映射与函数 X (数集或点集 ) 说明 在不同数学分支中有不同的惯用 X (≠ ) Y (数集) f f 称为X 上的泛函 X (≠ ) X f f 称为X 上的变换 R f f 称为定义在 X 上的函数 映射又称为算子. 名称. 例如