
第九节连续函数的运算与初等函数的连续性 一、连续函数的四则运算 二、反函数与复合函数的连续性 三、初等函数的连续性 上页 下页 返回 MathGS 公式 线与面 数学家
第九节 连续函数的运算与初等函数的连续性 一、连续函数的四则运算 二、反函数与复合函数的连续性 三、初等函数的连续性

第九节连续函数的运算与初等函数的连续性 一、连续函数的四则运算 定理1在某点连续的有限个函数经有限次和、差、 积、商(分母不为0)运算,结果仍是一个在该点连续的 函数. (利用极限的四则运算法则证明) 例如,Sinx,c0Sx都在(-oo,+oo)连续, sin x cOSx tanx= -cotx= 在其定义域内连续。 cos x sin x 上页 下页 返回 MathGS 公式 线与面 数学家
第九节 连续函数的运算与初等函数的连续性 一、连续函数的四则运算 在其定义域内连续. 定理1 在某点连续的有限个函数经有限次和 、差 、 ( 利用极限的四则运算法则证明) 积 、商(分母不为 0) 运算, 结果仍是一个在该点连续的 例如, 都在(- , + ) 连续, 函数

第九节连续函数的运算与初等函数的连续性 二、反函数与复合函数的连续性 1.反函数的连续性 定理2如果函数y=f(x)在区间I上单调增加(或单 调减少)且连续,那么它的反函数x=f)也在对应的 区间I,={y|y=fc),x∈Lx}上单调增加(或单调减少) 且连续。 证明略。 上页 下页 返回 MathGS 公式 线与面 数学家
第九节 连续函数的运算与初等函数的连续性 二、反函数与复合函数的连续性 定理2 如果函数 y = f (x) 在区间 Ix 上单调增加(或单 调减少)且连续,那么它的反函数 x = f -1 (y) 也在对应的 区间 Iy = { y | y = f (x) , x Ix } 上单调增加(或单调减少) 且连续. 证明略. 1. 反函数的连续性
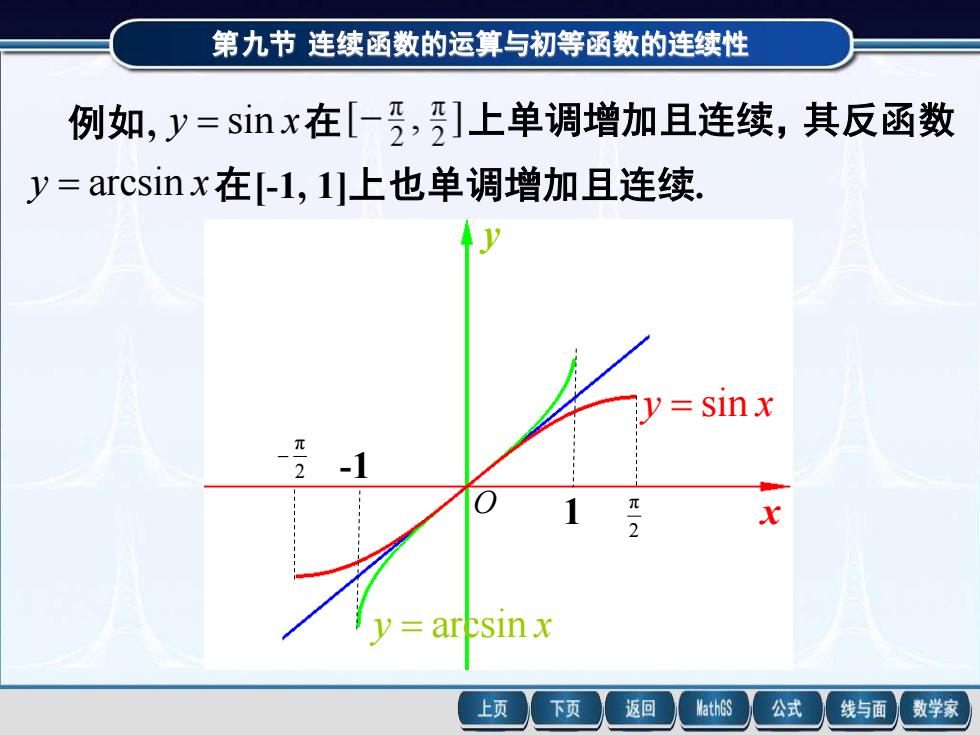
第九节连续函数的运算与初等函数的连续性 例如,y=sinx在[-乃,]上单调增加且连续,其反函数 y=arcsinx.在[-l,1]上也单调增加且连续, sinx π 上页 下页 返回 MathGS 公式 线与面 数学家
第九节 连续函数的运算与初等函数的连续性 例如, y = sin x 在 上单调增加且连续,其反函数 y = arcsin x 在[-1, 1]上也单调增加且连续. y = sin x y = arcsin x -1 1 2 π − 2 π x y O
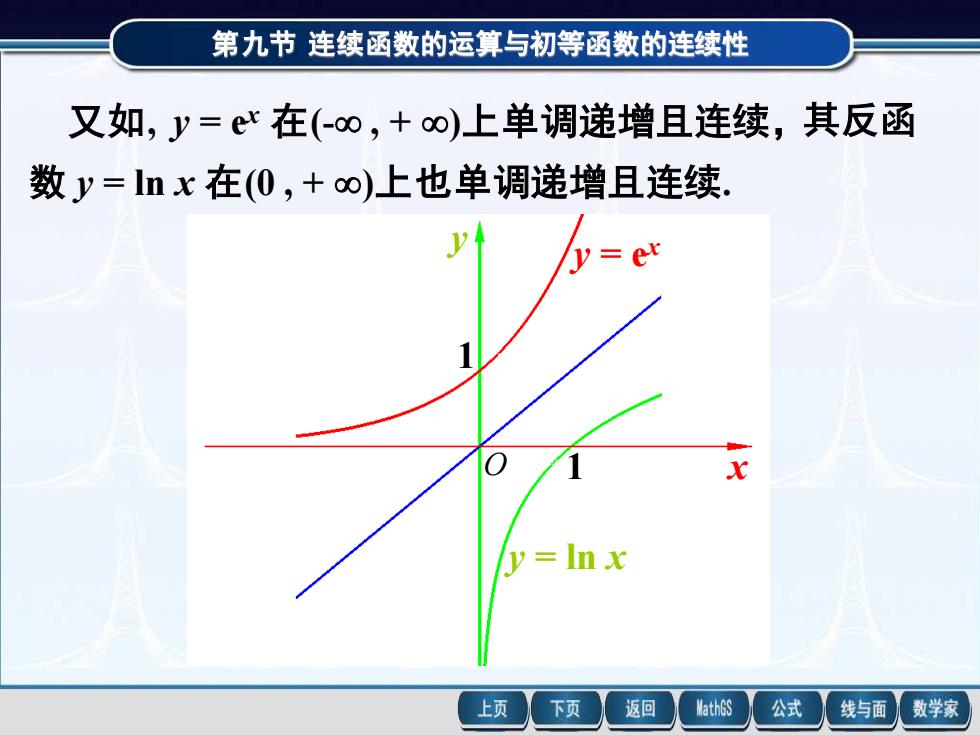
第九节连续函数的运算与初等函数的连续性 又如,y=ex在(-o,+o∞)上单调递增且连续,其反函 数y=lnx在(0,+o)上也单调递增且连续, er y=Inx 上页 下页 返回 MathGS 公式 线与面 数学家
第九节 连续函数的运算与初等函数的连续性 y = ex 在(- , + )上单调递增且连续, 数 y = ln x 在(0 , + )上也单调递增且连续. 又如, 其反函 y = ex y = ln x x y 1 1 O