《高等数学》课程教学资源（PPT课件）第一章函数与极限_第六节极限存在准则、两个重要极限

第六节极限存在准则两个重要极限 一、准则1第一重要极限 二、准则Ⅲ第二重要极限 *三、柯西极限存在准则 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 极限存在准则 两个重要极限 一、准则I 第一重要极限 二、准则II 第二重要极限 *三、柯西极限存在准则

第六节极限存在准则两个重要极限 一、准则1第一重要极限 准则I如果数列{xn}、{yn}及{zn}满足下列条件 (I)从某项起，即3no∈N,当n>n时，有 yn≤rn≤zn, 2) limy=a,limz=a, 1n-→o0 那么数列{xn}的极限存在，且limx,=a. 1n->0 证明 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 极限存在准则 两个重要极限 一、准则I 第一重要极限 准则I 如果数列 { xn }、{ yn } 及 { zn } 满足下列条件 (1) 从某项起，即  n0  N，当 n > n0 时，有 (2) , lim yn a n = → yn  xn  zn ， , lim zn a n = → 那么数列 { xn } 的极限存在，且 . lim x a n n = → 第六节 极限存在准则 两个重要极限 证明 (1) 当 n > n0 时， (2) , limyn a n = → yn  xn  zn ， , limzn a n = → . limxn a n = → y a n n = → lim  >0, N1 , 当 n > N1 时, 有 | yn – a | < , z a n n = → lim  >0, N2 , 当 n > N2 时, 有 | zn – a | <  , 已知当 n > n0 时，yn  xn  zn ， 取 N = max{ n0 , N1 , N2 }，则当n > N 时上述3个不等式 同时成立，从而有 yn  xn  z a –  < n < a +  , 即 | xn – a | <  . . limxn a n  = → 证毕

第六节极限存在准则两个重要极限 准则可以推广到函数的情形. 准则如果 1)当x∈J(xor) y4y=1 (或|x|>0时，8c)≤fx)≤h(x), sin x ys x (2)limg(x)=4,lim h(x)=4, =COSX X→x0 x→X0 (x→00)） (x→00) 那么limf(x)存在，且等A. x→x0 (x-→00) 准则及准则称为夹逼准则： 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 极限存在准则 两个重要极限 x y O 1 y =1 x x y sin = y = cos x 准则I可以推广到函数的情形. 准则I ' 如果 (1) 当 ( , ) 0 x U x r   (或 | x | > M)时，g(x)  f(x)  h(x) ， (2) ( ) , lim ( ) 0 g x A x x x = → → ( ) , lim ( ) 0 h x A x x x = → → 那么 ( ) lim ( ) 0 f x x x x → → 存在，且等 A . 准则I及准则I'称为夹逼准则

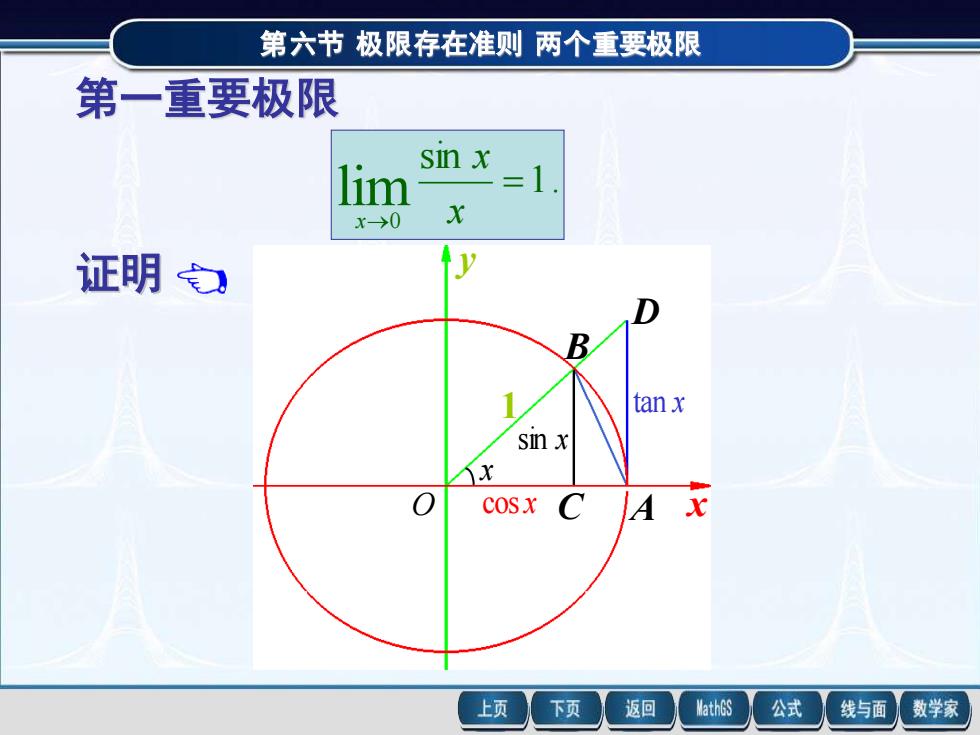
第六节极限存在准则两个重要极限 第一重要极限 sin x lim x→>0 X 证明之 B tanx six X COSX 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 极限存在准则 两个重要极限 第一重要极限 1. sin lim 0 = → x x x 第六节 极限存在准则 两个重要极限 O C A B D 1 sinx cosx tanx x x y 证明 右图中的圆为单位圆 AD 为切线，圆心角为 x ，且 , 2 π 0  x  BC ⊥ OA . 因为 , SAOB  S 扇形AOB  SAOD sin , 2 1 S x AOB = , 2 1 S x AOB 扇形 = tan , 2 1 S x 而 AOD = 所以 tan , 2 1 2 1 sin 2 1 x  x  x sin x  x  tan x , 1. sin cos   x x x O C A B D 1 sin x cos x tan x x x y

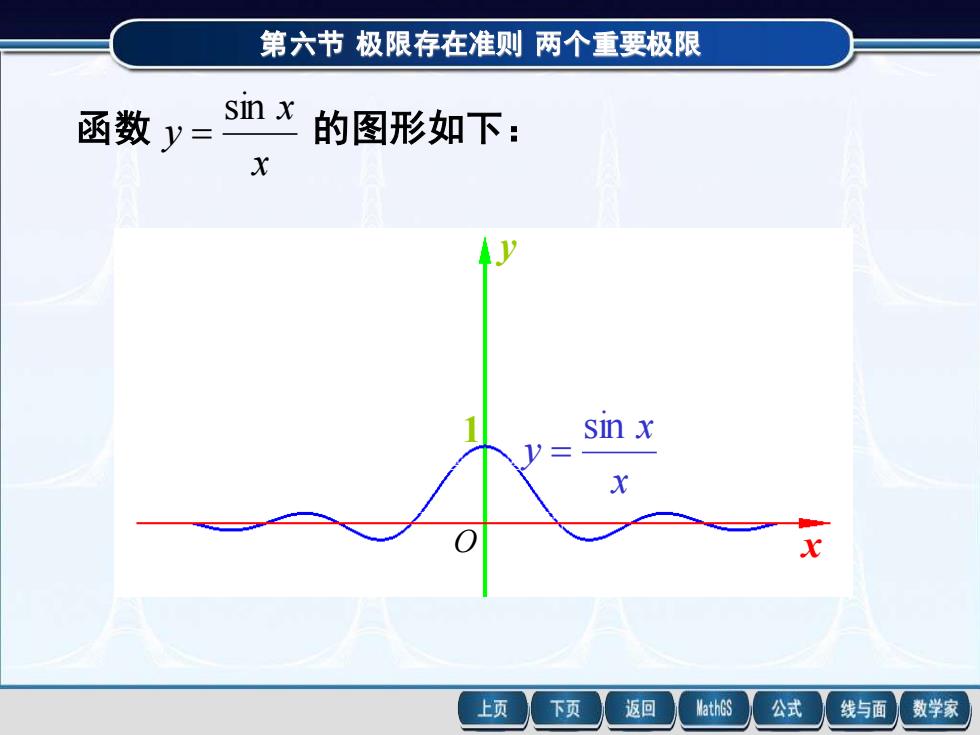
第六节极限存在准则两个重要极限 函数y=sn的图形如下： X sin x 上页 下页 返回 MathGS 公式 线与面 数学家

第六节 极限存在准则 两个重要极限 函数 x x y sin = 的图形如下： x x y sin = 1 x y O