
第七节无穷小的比较 一、无穷小的阶 二、无穷小等价的条件 三、利用等价无穷小求极限 上页 下页 返回 MathGS 公式 线与面 数学家
第七节 无穷小的比较 一、无穷小的阶 二、无穷小等价的条件 三、利用等价无穷小求极限
第七节无穷小的比较 一、无穷小的阶 当x→0时,下面4个函数都是无穷小: 3x,x,x2,sin x, 可它们趋于零的“速度”却不相同,这一点从下图中可 以清楚地看出.它们趋于零的 yly=3x y=Vx “速度”从低到高的顺序为 y=sin x x ,3x,sin x,x2. y=x2 但这种从图形来比较无穷小趋于 零的“速度”有时不够精确。 上页 下页 返回 MathGS 公式 线与面 数学家
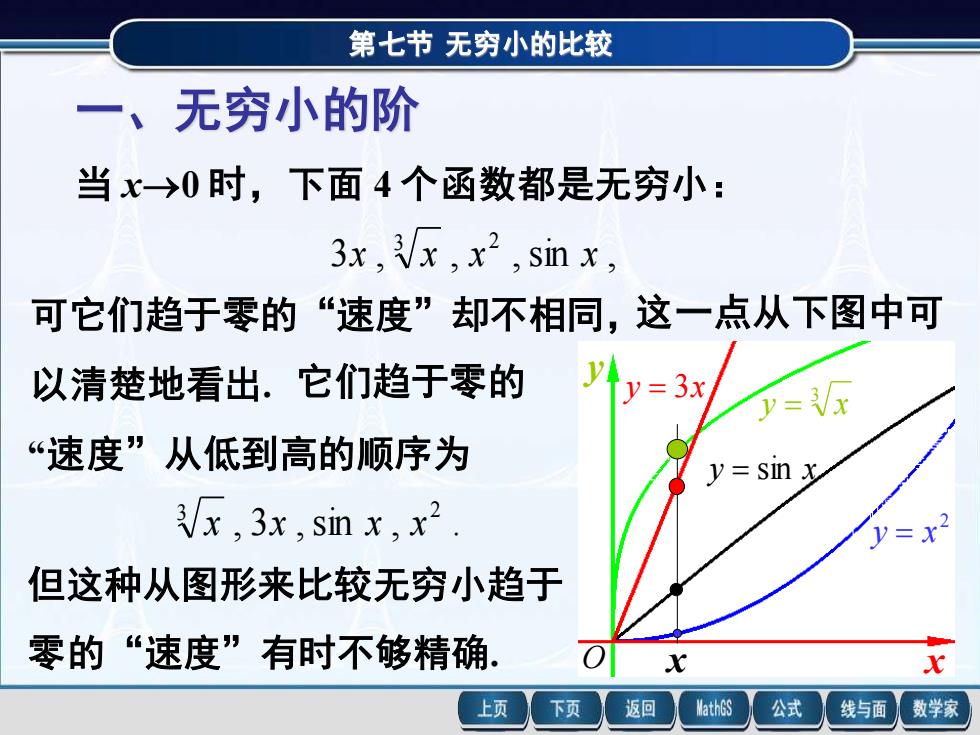
第七节 无穷小的比较 一、无穷小的阶 当 x→0 时,下面 4 个函数都是无穷小: 3 , , , sin , 3 2 x x x x 可它们趋于零的“速度”却不相同,这一点从下图中可 以清楚地看出. y = 3x 3 y = x 2 y = x y = sin x x x y O 它们趋于零的 “速度”从低到高的顺序为 , 3 , sin , . 3 2 x x x x 但这种从图形来比较无穷小趋于 零的“速度”有时不够精确

第七节无穷小的比较 x ,3x,sin x,x2 精确的方法是:用比值的极限来恒量它们趋于零的 “速度” 3x lim =0,所以趋于零的“速度”3x比“快”; x-→0 sin x 1 lim 所以趋于零的“速度”sinx与3x“相仿”; x→0 3x lim =0,所以趋于零的“速度”x2比sinx“快” →0 sin x 下面引进无穷小的阶,用来恒量趋于零的“速度” 上页 下页 返回 MathGS 公式 线与面 数学家
第七节 无穷小的比较 “相仿”; 精确的方法是:用比值的极限来恒量它们趋于零的 “速度”. , 3 , sin , . 3 2 x x x x 0 , 3 3 0 lim = → x x x 所以趋于零的“速度” 3 3x 比 x “快”; , 3 1 3 sin lim 0 = → x x x 所以趋于零的“速度” sin x 与 3x 0 , sin 2 0 lim = → x x x 所以趋于零的“速度” sin x 2 x 比 “快”. 下面引进无穷小的阶,用来恒量趋于零的“速度

第七节无穷小的比较 定义设lima=0,limB=0, 如果lim P=0,就说B是比a高阶的无穷小,记作 B=o(a);如果im E_o,就说B是比a低阶的无穷小 如果im E=c+0,就说B与a是同阶的无穷小 如果 lim =c*0,k>0, B 就说B是关于a的k阶 的无穷小 如果lim B-=1,就说B与a是等价无穷小,记作 a~B 上页 下页 返回 MathGS 公式 线与面 数学家
第七节 无穷小的比较 定义 设 lim = 0 , lim = 0 , 如果 lim = 0 , 就说 是比 高阶的无穷小,记作 = o() ; 如果 lim = , 就说 是比 低阶的无穷小. 如果 lim = c 0 , 就说 与 是同阶的无穷小; 如果 lim = c 0 , k 0 , k 的无穷小. 就说 是关于 的 k 阶 如果 lim = 1, 就说 与 是等价无穷小,记作 ~

第七节无穷小的比较 x ,3x,sin x,x2. 由定义可知,前面讨论过的上述4个无穷小中 x是比3x低阶的无穷小: 3x与sinx是同阶无穷小; x2是比sinx高阶的无穷小; x2是关于sinx2阶的无穷小. 上页 下页 返回 MathGS 公式 线与面 数学家
第七节 无穷小的比较 , 3 , sin , . 3 2 x x x x 由定义可知, 前面讨论过的上述4个无穷小中 3 x 3x sin x 2 x 是比 低阶的无穷小; 3x 与 是同阶无穷小; 是比 sin x 高阶的无穷小; 2 x 是关于 sin x 2阶的无穷小