
第十节闭区间上连续函数的性质 一、有界性与最大值最小值定理 二、零点定理与介值定理 *三、一致连续性 上页 下页 返回 MathGS 公式 线与面 数学家
第十节 闭区间上连续函数的性质 一、有界性与最大值最小值定理 二、零点定理与介值定理 *三、一致连续性
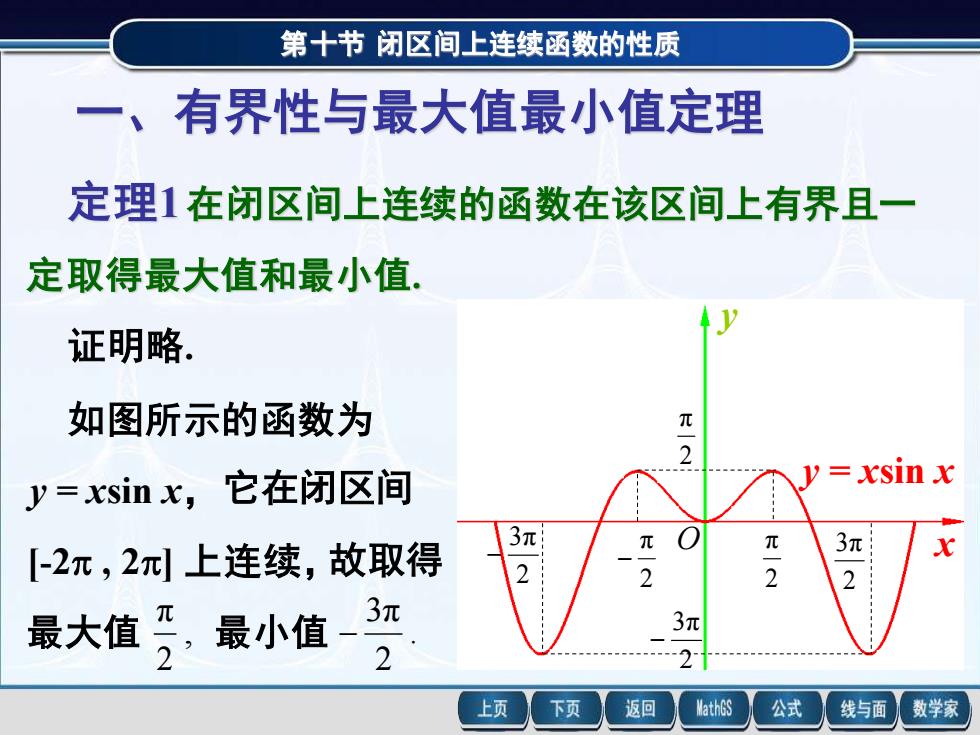
第十节闭区间上连续函数的性质 一、有界性与最大值最小值定理 定理1在闭区间上连续的函数在该区间上有界且一 定取得最大值和最小值。 证明略。 如图所示的函数为 π 2 y=xsin x,它在闭区间 y=xsin x 3π [-2π,2π上连续,故取得 2 3 2 2 2 爱大值于最小值-习 3π 上页 下页 返回 MathGS 公式 线与面 数学家
第十节 闭区间上连续函数的性质 一、有界性与最大值最小值定理 定理1在闭区间上连续的函数在该区间上有界且一 定取得最大值和最小值. 证明略. 如图所示的函数为 y = xsin x,它在闭区间 [-2 , 2] 上连续,故取得 最大值 , 2 π 最小值 . 2 3π − x y y = xsin x 2 3π − 2 π − 2 π 2 3π 2 π 2 3π − O
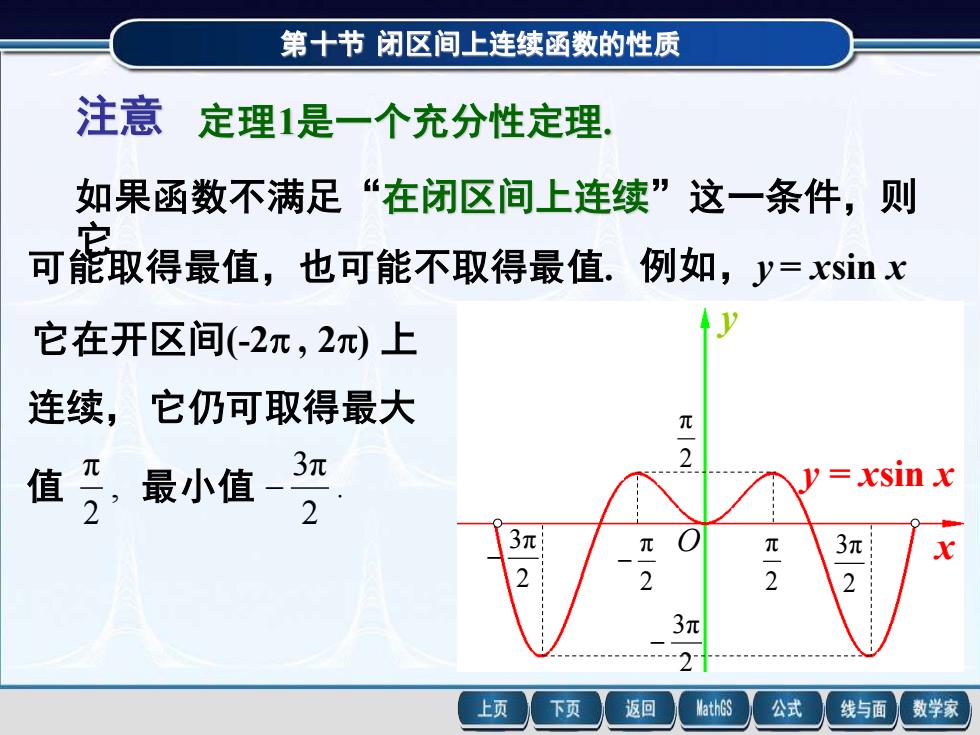
第十节闭区间上连续函数的性质 注意 定理1是一个充分性定理, 如果函数不满足“在闭区间上连续”这一条件,则 应 可能取得最值,也可能不取得最值.例如,y=xsin 它在开区间(-2π,2π)上 连续,它仍可取得最大 π 2 乃,最小 值 、 3元 y=xsin x 3π 2 3π 2 2 2 2 3π 2 上页 下页 返回 MathGS 公式 线与面 数学家
第十节 闭区间上连续函数的性质 注意 定理1是一个充分性定理. 如果函数不满足“在闭区间上连续”这一条件,则 它 可能取得最值,也可能不取得最值. 例如,y = xsin x 它在开区间(-2 , 2) 上 连续, 它仍可取得最大 值 , 2 π 最小值 . 2 3π − x y y = xsin x 2 3π − 2 π − 2 π 2 3π 2 π 2 3π − O

第十节闭区间上连续函数的性质 又如,y=x2sinx它在开区间(-1.5,1.5)上连续,但它不 取得最大值和最小值. yx2sin x -1.5 1.5 上页 下页 返回 MathGS 公式 线与面 数学家
第十节 闭区间上连续函数的性质 又如,y = x 2 sin x 它在开区间(-1.5 , 1.5) 上连续, 但它不 取得最大值和最小值. x y y = x 2 sin x -1.5 O 1.5

第十节闭区间上连续函数的性质 再如,函数 -x+1,0≤x<1 y=f(x)= 1, x=1, -x+3,1<x≤2 2 x 在闭区间0,2]上有间断点x=1,这函数fx)在闭区 间0,2]上虽然有界,但是既无最大值又无最小值. 上页 下页 返回 MathGS 公式 线与面 数学家
第十节 闭区间上连续函数的性质 再如,函数 − + = − + = = 3, 1 2 1, 1, 1, 0 1, ( ) x x x x x y f x 在闭区间 [0 , 2] 上有间断点 x = 1,这函数 f (x) 在闭区 间 [0 , 2] 上虽然有界,但是既无最大值又无最小值. x y 1 1 2 O 2