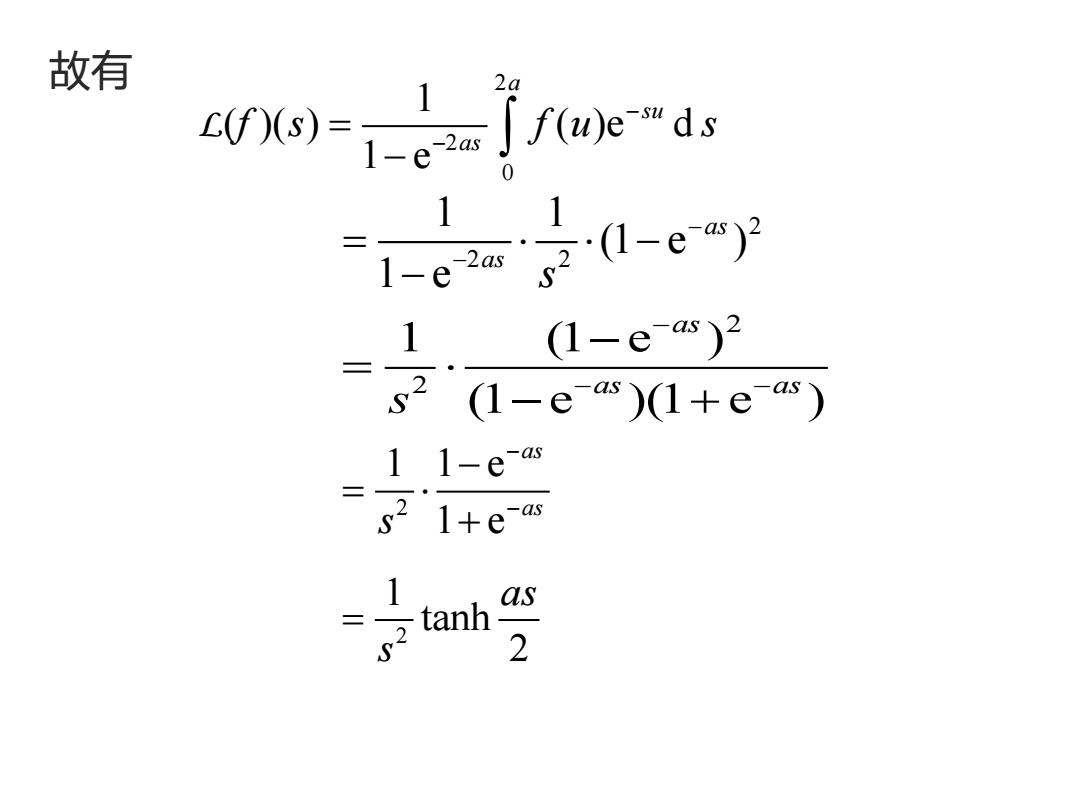
故有 ((s)= dw2-ey 1 (1-eas)2 s2(1-ea)1+ea) 11-es 二 s21+e 1
故有 2 2 0 1 ( )( ) ( )e d 1 e a su as f s f u s − − = − L 2 2 2 1 1 (1 e ) 1 e as as s − − = − − 2 2 1 (1 e ) (1 e )(1 e ) as as as s − − − − = − + 2 1 1 e 1 e as as s − − − = + 2 1 tanh 2 as s =

单位脉冲函数)的拉普拉斯变换 00 c[o](s)=∫δ(t)edt 0、 例8.6求单位脉冲函数t)的拉普拉斯变换 解:c[f](s)=「6(t)edt 0 00 8(t)e-"dt -00 =eo=1
单位脉冲函数(t)的拉普拉斯变换 0 ( ) ( )e st s t dt − − = L 例8.6 求单位脉冲函数(t)的拉普拉斯变换. 解: 0 ( ) ( )e d st f s t t − − = L ( )e d st t t − − = 0 e 1 st t − = = =

§8.2拉普拉斯变换的性质 定理8.2对函数的拉普拉斯变换有下列性质成立 (1)(线性性质)设a,B为常数,记F(s)=c[f](s) G(s)=c[8](s),则有 L af+Bg(s)=aF(s)+BG(s) 或有 Laf+Bg(t)=aF(t)+BG(t) (2)(延迟性质)荐[f](s)=F(s),则对t。>0,有 L f(t-t)(s)=e F(s) 或有 e-so F(t)=f(t-to) (3)(位移性质)记r[(s)=F(s)对常数s,若 Re(s-s)>o。,则有 Ce f(s)=F(s-50)
§8.2 拉普拉斯变换的性质 定理8.2 对函数的拉普拉斯变换有下列性质成立. (1)(线性性质)设,为常数,记 , ,则有 或有 (2)(延迟性质)若 ,则对 ,有 或有 (3)(位移性质)记 .对常数s0,若 ,则有 F s f s ( ) ( ) = L G s g s ( ) ( ) = L L f g s F s G s + = + ( ) ( ) ( ) 1 f g t F t G t ( ) ( ) ( ) − L + = + L f s F s ( ) ( ) = 0 t 0 0 0 ( ) ( ) e ( ) st f t t s F s − L − = 1 0 0 e ( ) ( ) st F t f t t − − = − L L f s F s ( ) ( ) = Re( )0 0 s s − 0 0 e ( ) ( ) s t f s F s s = − L

证明:性质1说明函数的线性组合的拉普拉斯变换等 于各函数的拉普拉斯变换的线性组合 证明性质2 当K0时,有f()=0,所以当t<时,f(t-t)=0 因此有 c[fu-o]=∫fu-4o)e"dl 00 =f(t-t)e-dt 00 =∫f(w)eso)du =e∫f(u)e"du=e%F(s)
证明: 性质1说明函数的线性组合的拉普拉斯变换等 于各函数的拉普拉斯变换的线性组合. 证明性质2 当t<0时,有 ,所以当 时, 因此有 f t( ) 0 = 0 t t 0 f t t ( ) 0, − = 0 0 0 ( ) ( )e d st f t t f t t t − − = − L 0 0 ( )e d st t f t t t − = − 0 ( ) 0 ( )e d s u t f u u − + = 0 0 e ( )e d st su f u u − − = 0 e ( ) st F s − =