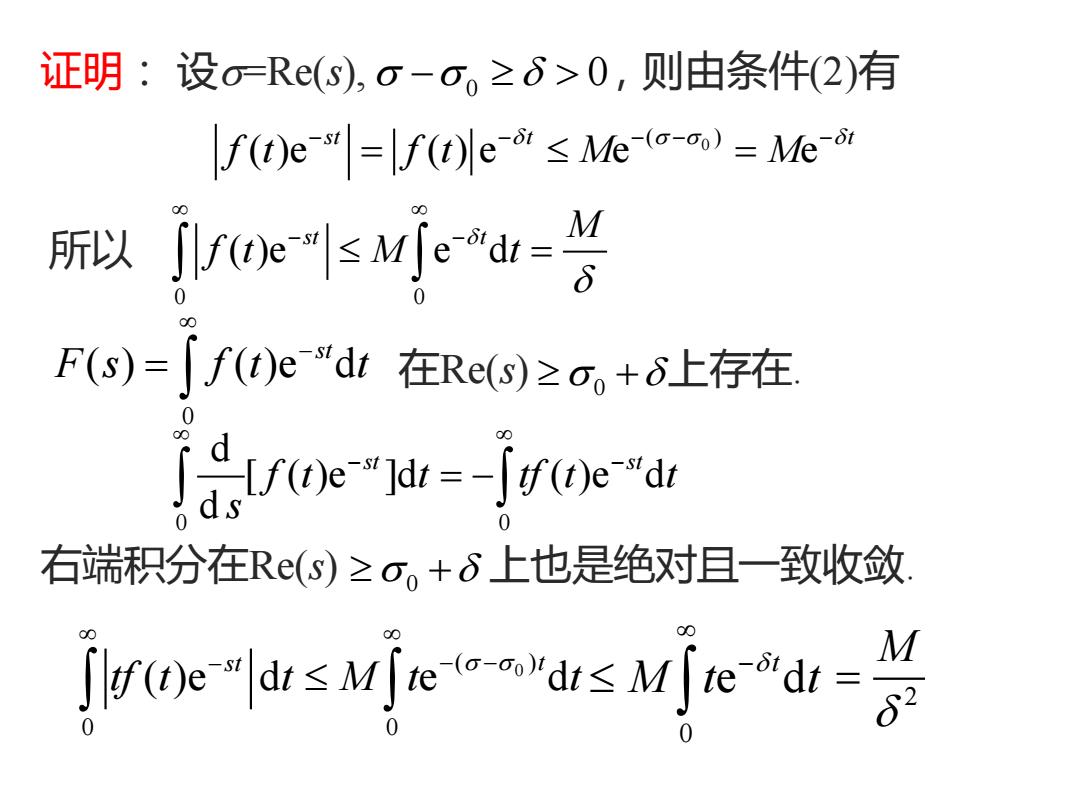
证明:设o-R(s),o-o。≥6>0,则由条件(2)有 f(u)e=f(le-m≤Meo-o)=Mea 所以- M F(s)=f(t)edt在Re(s)≥o。+6上存在 0 oe=-jgoeu 0 右端积分在R(s)≥o。+6上也是绝对且一致收敛 可= M
证明: 设=Re(s), − 0 0 ,则由条件(2)有 0 ( ) ( )e ( ) e e e st t t f t f t M M − − − − − = = 所以 0 0 ( )e e d st t M f t M t − − = + 0 0 ( ) ( )e dst F s f t t − = 在Re(s) 上存在. 0 0 d [ ( )e ]d ( )e d d st st f t t tf t t s − − = − 右端积分在Re(s) 上也是绝对且一致收敛. + 0 0 ( ) 0 0 ( )e d e d st t tf t t M t t − − − 0 e dt M t t − 2 M =

积分与微分的次序可以交换,于是有 品o=fwnean-jwe1u-joe*ar 由拉普拉斯变换的定义,得 F'(s)=L[(-t)f(t)](s) 所以F'(s)在R(s)≥o。+6上可导 由的任意性知,F(s在R(s)>o上存在,且为解析 函数.定理得证
积分与微分的次序可以交换,于是有 0 d d ( ) ( )e d d d st F s f t t s s − = 0 d [ ( )e ]d d st f t t s − = 0 ( ) ( )e d st t f t t − = − 由拉普拉斯变换的定义,得 F s t f t s ( ) L[( ) ( )]( ) = − 所以, F s ( ) 在 上可导. Re( ) 0 s + 由的任意性知, 在 上存在,且为解析 函数. 定理得证. F s( ) Re( ) 0 s

例8.4求正弦函数sin的拉普拉斯变换,其中为实数 解:当Re(s)>O时,有 ● [sin kt](s)=sin ktedt -st e Fg2+k(-y-sin-k-cosk) 0 k S2+k2 余弦函数cosk的拉普拉斯变换 c[cos() Re(s)>0
例8.4 求正弦函数sinkt的拉普拉斯变换,其中k为实数. 解:当 Re( ) 0 s 时,有 0 sin ( ) sin e d st kt s kt t − = L 2 2 0 e ( sin cos ) st s kt k kt s k − = − − + 2 2 k s k = + 余弦函数coskt的拉普拉斯变换 2 2 cos ( ) s kt s s k = + L Re( ) 0 s
孙s5求周期为2的函数f0-2a-4,a51<2a, t, 0≤t<, 的拉普拉斯变换 解:由拉普拉斯变换的定义, 有 c[f]s)=∫f)e"dt 2a 3a 4a 2a 4a 6a 2(k+1)a "+fe+fedt+f(e"di 2a 2 ka 00 2(k+1)a ∑」f(t)edt k=0 2ka 令t=u++2ka,则有 2(k+1)a 2a 2a ∫f)e"dt=jfu+2ka)eu*adee2ka∫fw)e"du 2ka
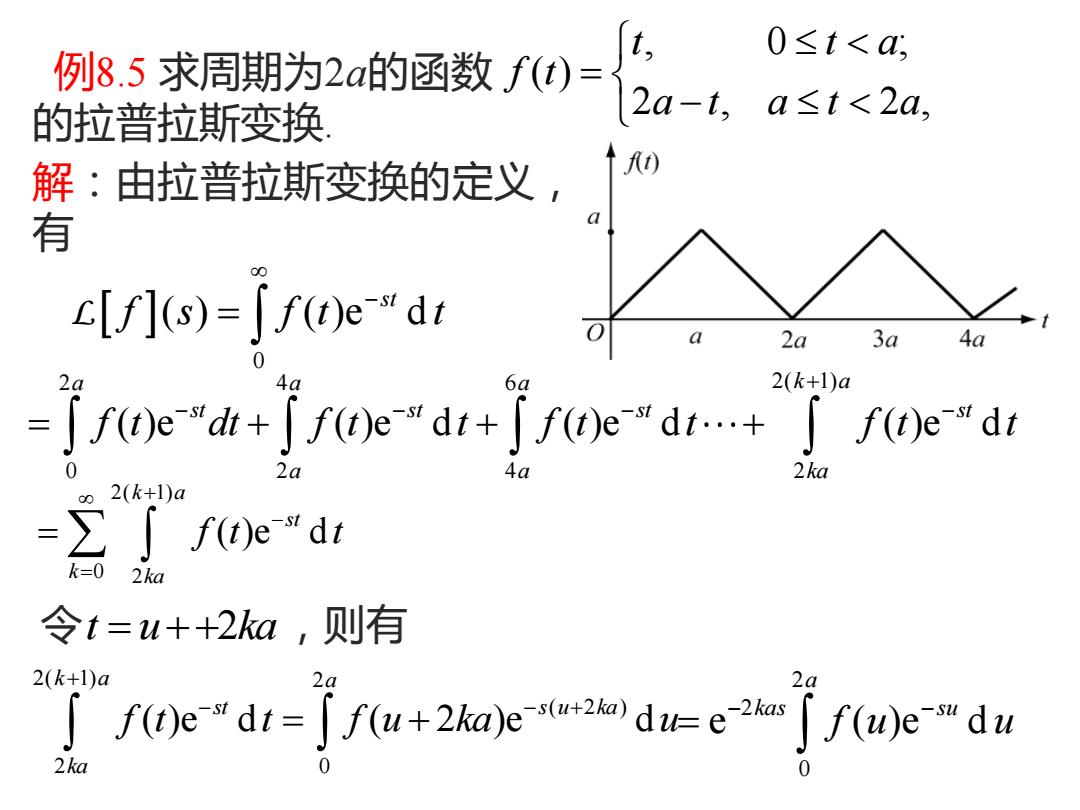
例8.5 求周期为2a的函数 的拉普拉斯变换. , 0 ; ( ) 2 , 2 , t t a f t a t a t a = − 解:由拉普拉斯变换的定义, 有 0 ( ) ( )e d st f s f t t − = L 2 4 6 2( 1) 0 2 4 2 ( )e ( )e d ( )e d ( )e d a a a k a st st st st a a ka f t dt f t t f t t f t t + − − − − = + + + 2( 1) 0 2 ( )e d k a st k ka f t t + − = = 令 t u ka = + +2 ,则有 2( 1) 2 ( 2 ) 2 0 ( )e d ( 2 )e d k a a st s u ka ka f t t f u ka u + − − + = + 2 2 0 e ( )e d a kas su f u u − − =

根据函数的定义,有 2a udu=jedu+了rea-wed}a-e 0 2a 所以,c[f]s)=∑e2jfe"du k=0 2a -fuedu 记B=Re(s)当B>0时,有e2a=e2aB<1 因此有 1 = k=0 1-e-2as
根据函数的定义,有 2 2 0 0 0 ( )e d e d (2 )e d a a a su su su f u u u u f a u u − − − = + − 2 2 1 (1 e ) as s − = − 所以, 2 2 0 0 ( ) ( )e d a kas su k f s e f u u − − = = L 2 2 0 0 ( )e d e a su kas k f u u − − = = 记 = Re( )s . 当 0 时,有 2 2 e e 1 − − as a = 因此有 2 2 0 1 e 1 e kas as k − − = = −