
概率论与数理统 第五章大数定律与中心极限定理 第一节 大数定律 第二节 中心极限定理
第五章 大数定律与中心极限定理 第一节 大数定律 第二节 中心极限定理

概率论与数理统计 第一节大数定律 切比雪夫不等式 设随机变量X存在有限方差D(),则对任意正数ε,有 P明x-0≥4≤X0或x-F<≥ X) 定义5.1设随机变量1,Y,,Ym,…是一个随机变量 序列,a是一个常数若对于任意正数有 lim PY,-a<)=1, 则称序列Y1,Y,,Y,…依概率收敛于,记为 YnP→a. 上一页 下一页 返回
第一节 大数定律 定义5.1 上一页 下一页 返回
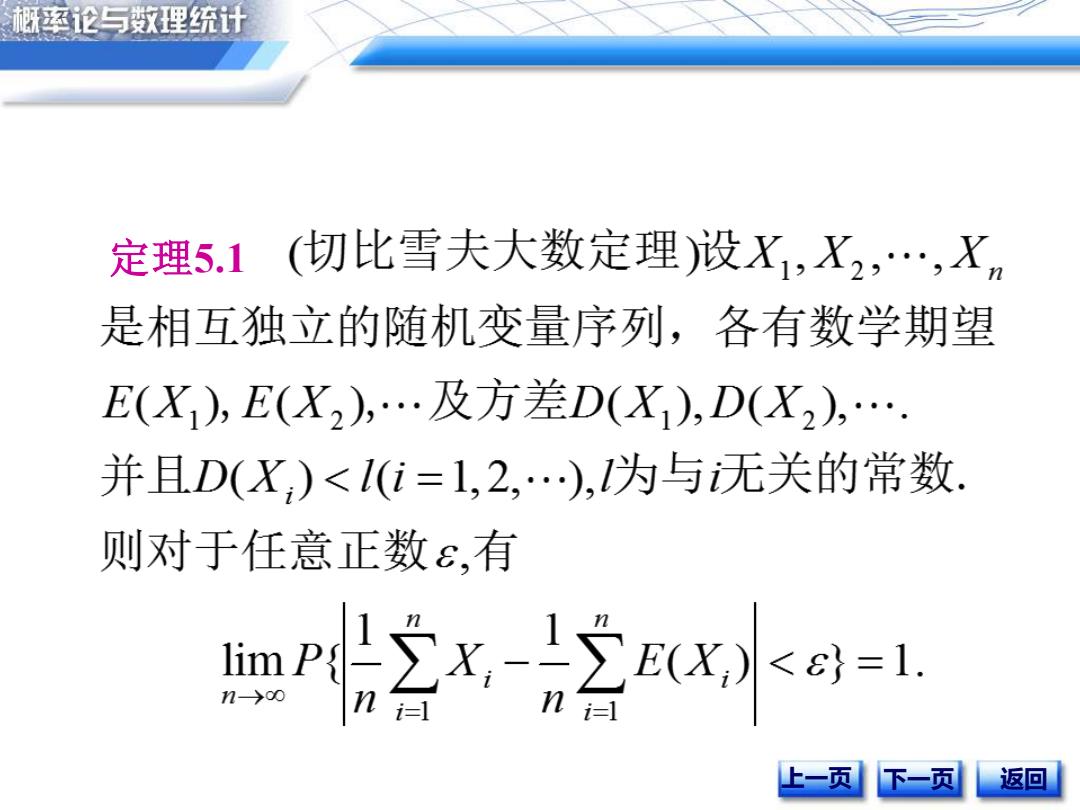
概率论与数理统计 定理5.1 (切比雪夫大数定理)设X1,X2,…,X, 是相互独立的随机变量序列,各有数学期望 E(X),E(X2),…及方差D(X),D(X2),…. 并且D(X)<1(i=1,2,),1为与无关的常数。 则对于任意正数,有 P哈2名空ix)=1 上一页 下一页 返回
定理5.1 上一页 下一页 返回

概率论与数理统计 定理5.2(切比雪夫定理的特殊情况设随机变量 X,X2,…,Xn,…相互独立,且具有相同的数学 期望和方差:E(X)=4,D(Xx)=o2(k=1,2,…) 作前个随机变量的算术平均 y=12x 1nk-1 则对于任意正数有 lim P{Y,-u<a=1 上一页 下一页 返回
定理5.2 上一页 下一页 返回

概率论与数理统计 定理5.3 (伯努利大数定律)以n4是n次独立重复试 验中事件A出现的次数.D是事件A在每次试验中发生的 概率(0<p<),则对任意的ε>0有: mP%- e-0或mr-1 证明:设X,表示第i次试验中事件A出现的次数, =1,2,n,则X,X2,Xn相互独立且均服从参数为p的 0-1)分布,故有EX)=p,DX=p(1-p )i=1,2,.,n 且”4=∑X;,由契比雪夫大数定律知,对于任意 的&>0,有mP-2=imP2x-22线=0 上一页 下一页 回
或 证明:设Xi表示第i 次试验中事件A出现的次数, i=1,2,…,n,则X1 ,X2 ,…,Xn相互独立且均服从参数为p的 (0-1)分布,故有 E(Xi )=p, D(Xi )=p(1-p) i=1,2,…,n 且 ,由契比雪夫大数定律知,对于任意 的 ,有 (伯努利大数定律)以nA是n次独立重复试 验中事件A出现的次数. p是事件A在每次试验中发生的 概率 (0<p<1),则对任意的 >0有: 定理5.3 上一页 下一页 返回