
概率论与数理统道 第四章 随机变量的数字特征 第一节 数学期望 第二节 方差 第三节 协方差与相关系数 第四节 矩、协方差矩阵
第四章 随机变量的数字特征 第一节 数学期望 第二节 方差 第三节 协方差与相关系数 第四节 矩、协方差矩阵

概率论与数理统计 第一节 数学期望 1.数学期望的定义 定义4.1设离散型随机变量X的分布律为 PX=XR=PR k=1,2,.… 若级数∑xP绝对收敛,则称级数∑xxP k=1 k=1 为随机变量X的数学期望,简称期望,记为EX),即 00 E(X)=∑XP k=1 上一页 下一页 返回
上一页 下一页 返回 第一节 数学期望 定义4.1 为随机变量X的数学期望,简称期望,记为E(X),即 1.数学期望的定义

概率论与数理统计 设连续型随机变量X具有概率密度f(x) 若∫xf(x)绝对收敛,则称积分∫f(x)为X的 数学期望,记为E(X),即E(X)=f(x) EX)是一个实数,形式上是X的可能值的加权 平均数,实质上它体现了X取值的真正平均。又称 EX)为X的平均值,简称均值。它完全由X的分布 所决定,又称为分布的均值 上一页 下一页 返回
上一页 下一页 返回 E(X)是一个实数,形式上是X的可能值的加权 平均数,实质上它体现了X取值的真正平均。又称 E(X)为X的平均值,简称均值。它完全由X的分布 所决定,又称为分布的均值

概率论与效理统计 例4.1某商店在年末大甩卖中进行有奖销售,摇奖时 从摇箱摇出的球的可能颜色为:红、黄、蓝、白、黑 五种,其对应的奖金额分别为:10000元、1000元、 100元、10元、1元.假定摇箱内装有很多球,其中红、 黄、蓝、白、黑的比例分别为: 0.01%,0.15%,1.34%,10%,88.5%,求每次摇奖摇出的 奖金额X的数学期望! 解每次摇奖摇出的奖金额X是一个随机变量,易知 它的分布律为 X 10000 1000 100 10 1 Pk 0.0001 0.0015 0.0134 0.1 0.885 上一页 下一页 返回
上一页 下一页 返回 例4.1 某商店在年末大甩卖中进行有奖销售,摇奖时 从摇箱摇出的球的可能颜色为:红、黄、蓝、白、黑 五种,其对应的奖金额分别为:10000元、1000元、 100元、10元、1元.假定摇箱内装有很多球,其中红、 黄、蓝、白、黑的比例分别为: 0.01%,0.15%,1.34%,10%,88.5%,求每次摇奖摇出的 奖金额X的数学期望. 解 每次摇奖摇出的奖金额X是一个随机变量,易知 它的分布律为 X 10000 1000 100 10 1 pk 0.0001 0.0015 0.0134 0.1 0.885
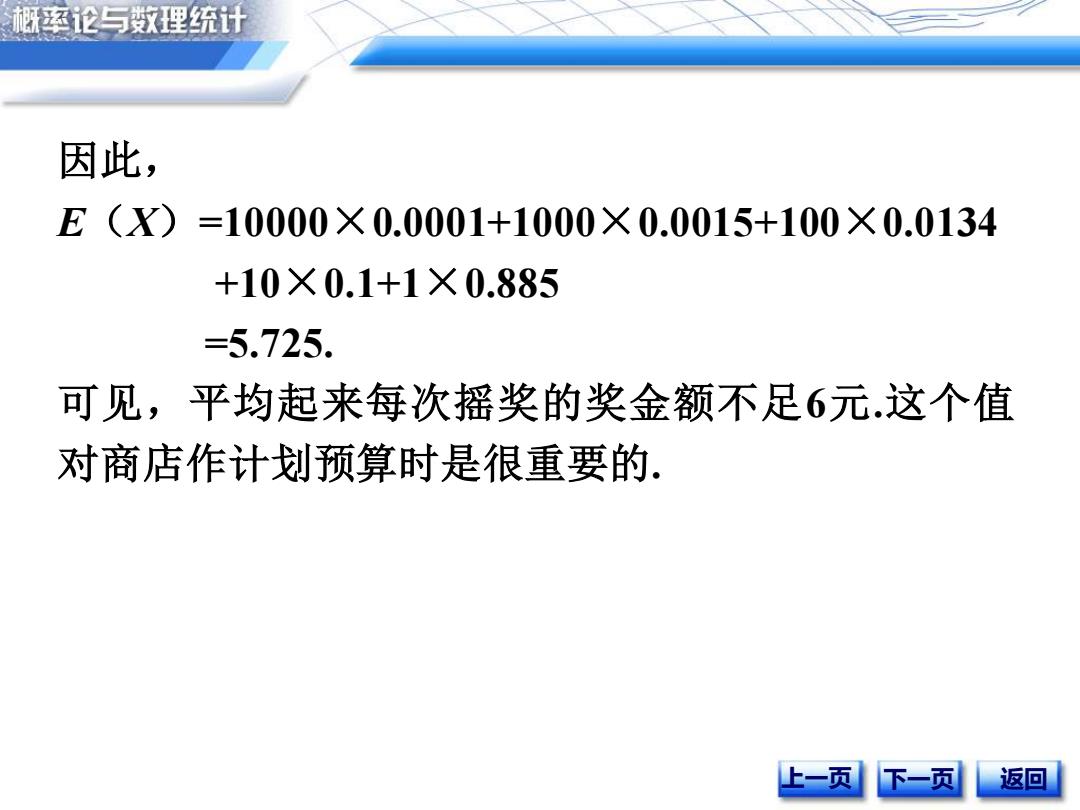
概率论与数理统计 因此, E(X)=10000×0.0001+1000×0.0015+100×0.0134 +10×0.1+1×0.885 =5.725. 可见,平均起来每次摇奖的奖金额不足6元.这个值 对商店作计划预算时是很重要的. 上一页下一页 返回
上一页 下一页 返回 因此, E(X)=10000×0.0001+1000×0.0015+100×0.0134 +10×0.1+1×0.885 =5.725. 可见,平均起来每次摇奖的奖金额不足6元.这个值 对商店作计划预算时是很重要的