第七章 傅里叶变换

§7.1傅里叶变换 一个以L为周期的函数f(t),如果在区间[-L/2,L/2]上 连续,那么在[-L/2,L/2]上可以展开成傅里叶级数 f.(0)=4+∑(a,cos not+b,sinnot), n=] 其中 2元 2 L/2 0= ,ao 「f(t)dt, L L/2 2 An L 」fi(t)cosnotdt,.n=1,2,…, -L/2 L/2 b 2 」f2(t)sin noidt,.n=1,2,…. L -L/2 一个周期函数表示成正弦函数类的和,称为函数f() 的傅里叶级数
§7.1 傅里叶变换 一个以L为周期的函数fL (t),如果在区间[-L/2,L/2]上 连续,那么在[-L/2,L/2]上可以展开成傅里叶级数 其中 一个周期函数表示成正弦函数类的和,称为函数fL (t) 的傅里叶级数. 0 1 ( ) ( cos sin ), 2 L n n n a f t a n t b n t = = + + / 2 0 / 2 / 2 / 2 / 2 / 2 2π 2 , ( )d , 2 ( )cos d , 1,2, , 2 ( )sin d , 1,2, . L L L L n L L L n L L a f t t L L a f t n t t n L b f t n t t n L − − − = = = = = =

傅里叶级数的复指数形式 e"+e e”+ei cost sint =一1 2 2i 2 f(0)= +e一+b,eo、 e n=1 2 2i a。-b+&,ti6em 2 2 2i L/2 记 -L/2
傅里叶级数的复指数形式 i i i i i i e e e e e e cos sin i , 2 2i 2 t t t t t t t t − − − + + + = = = − i i i i 0 1 0 i i 1 e e e e ( ) 2 2 2i i i e e . 2 2 2i n t n t n t n t L n n n n n n n n t n t n a f t a b a a b a b − − = − = + + = + + − + = + + / 2 0 0 / 2 1 ( )d , 2 L L L a c f t t L − = = 记
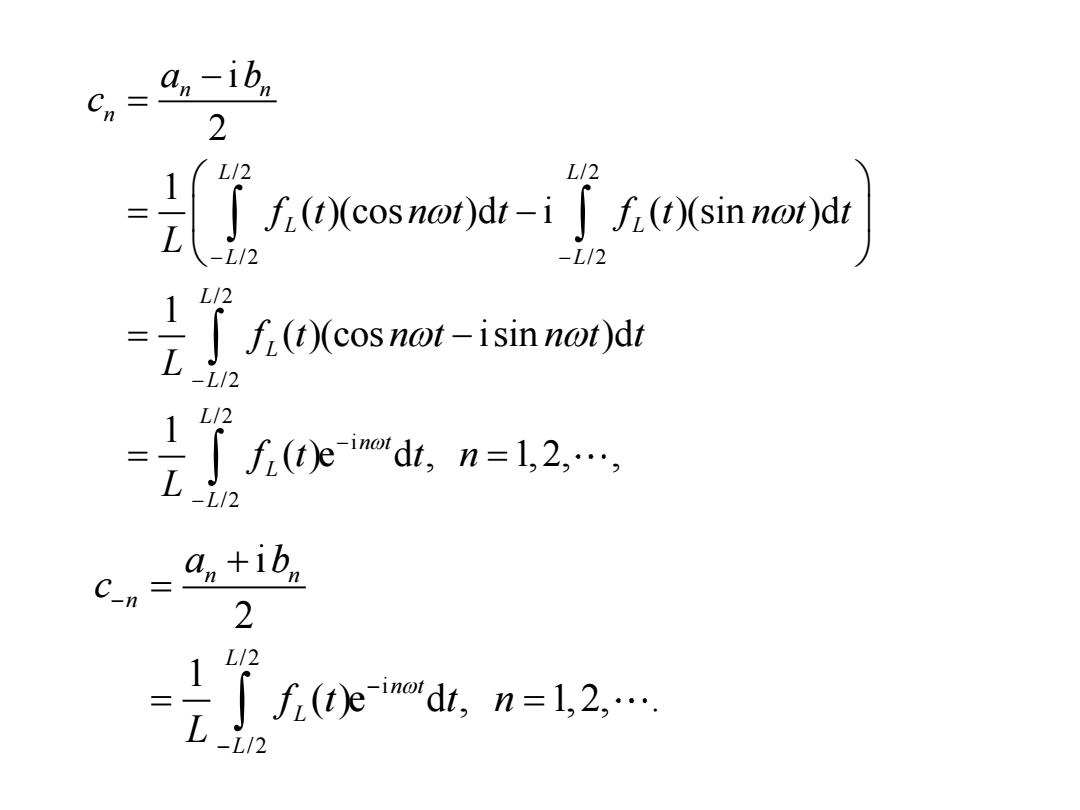
an Cn 2 L/2 L/2 是了f.(Xcosnor)-i了f.()dt -L/2 1 L/2 f(t)(cosnot-isinnot)dt -L/2 Jf0ed业,n=l2,, 1 L12 -L/2 Cn= an+ibn 2 .2. L2 L/2
/2 /2 /2 /2 / 2 / 2 / 2 i / 2 i 2 1 ( )(cos )d i ( )(sin )d 1 ( )(cos isin )d 1 ( )e d , 1,2, , n n n L L L L L L L L L L n t L L a b c f t n t t f t n t t L f t n t n t t L f t t n L − − − − − − = = − = − = = / 2 i / 2 i 2 1 ( )e d , 1,2, . n n n L n t L L a b c f t t n L − − − + = = =
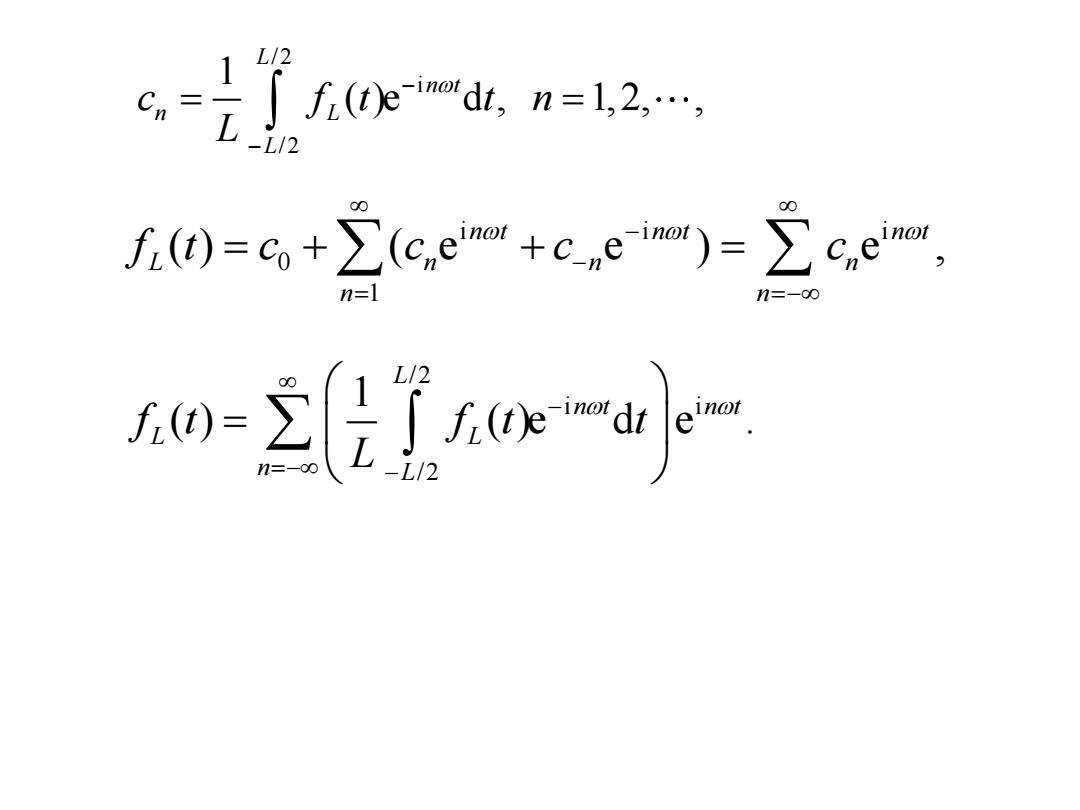
=气emn=l2. L72 -L/2 f0=G,+∑c,ew+cem)=∑c,e, n=] n=-o0 0-wj
/ 2 i / 2 1 ( )e d , 1,2, , L n t n L L c f t t n L − − = = i i i 0 1 ( ) ( e e ) e , n t n t n t L n n n n n f t c c c c − − = =− = + + = / 2 i i / 2 1 ( ) ( )e d e . L n t n t L L n L f t f t t L − =− − =