
第二章 解析玉数

§2.1复变函数的概念、 极限与连续性 1.复变函数的概念 定义2.1设E为一复数集若对E中的每一个复数z=x+iy 按照某种法则有确定的一个或几个复数w=u+v与 之对应,那么称复变数w是复变数的函数(简称复变 函数),记作 w=f(z) 通常也称w=z)为定义在E上的复变函数,其中称为 定义域,E中所有的z对应的一切w值构成的集合称为 z)的值域,记作)或G. 若的一个值对应着w的一个值,则称复变函数几z) 是单值的;若z的一个值对应着的两个或两个以上的 值,则称复变函数)是多值的
§2.1 复变函数的概念、极限与连续性 1. 复变函数的概念 定义2.1 设E为一复数集.若对E中的每一个复数 ,按照某种法则f有确定的一个或几个复数 与 之对应,那么称复变数w是复变数z的函数(简称复变 函数),记作 . 通常也称w=f(z)为定义在E上的复变函数,其中E称为 定义域,E中所有的z对应的一切w值构成的集合 称为 f(z)的值域,记作 f(E) 或G. z x y = + i w u v = +i w f z = ( ) 若z的一个值对应着w的一个值,则称复变函数 f(z) 是单值的;若z的一个值对应着w的两个或两个以上的 值,则称复变函数 f(z)是多值的
复数=x+iy与w=u+iv分别对应实数对(x,y)和(u,v), 对于函数w=z),u、v为x、y的二元实数函u(x,y)和 vx,y),所以w=z)又常写成w=u(x,y)十iv(x,y)。 函数w=z2+1.令=x+iy,w=u什iv,那么 w=u+i=(x+iy)2+1=x2-y2+1+2xy1, w=z2+1对应于两个实函数=x2-y2+1和=2xy. 对于复变函数w=z)即u+i=fx+iy),可以理解为 两个复平面上的点集之间的映射,具体地说,复变 函数w=孔z)给出了z平面上的点集到w平面上的点集 E)或G)之间的一个对应关系: Vz∈E→w∈f(z)∈G 其中w称为z的像, z平面 w平面 z称为w的原像 w=f(z) u
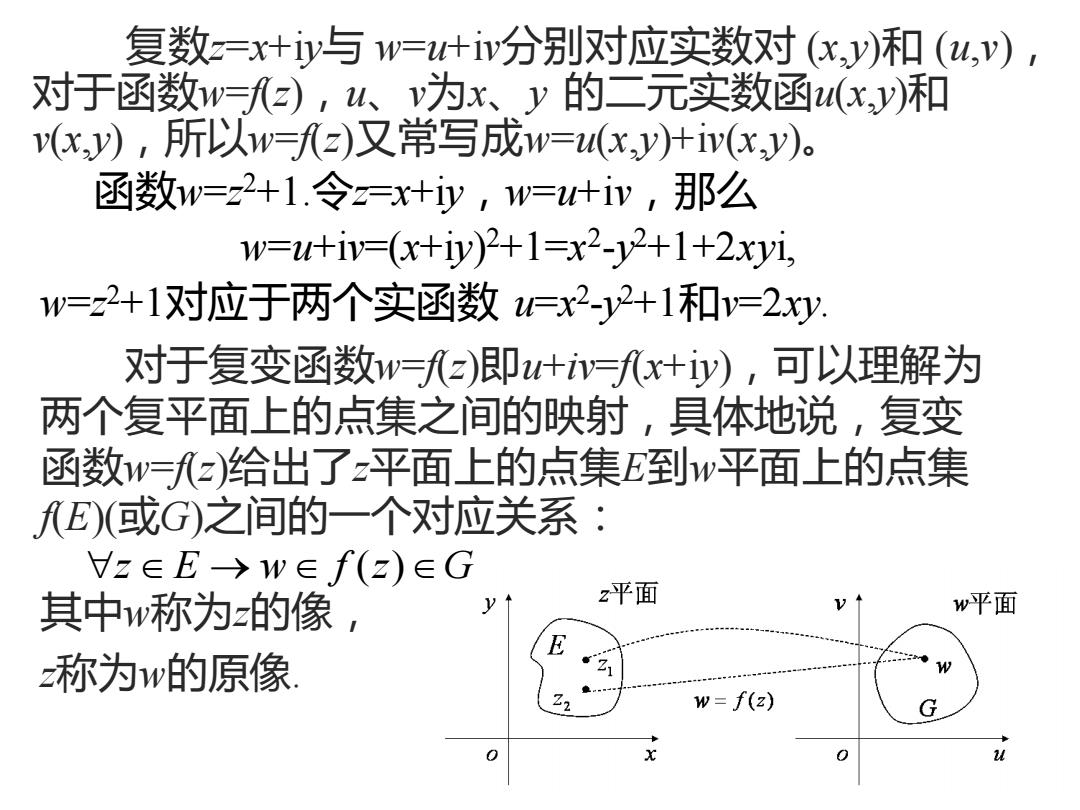
复数z=x+iy与 w=u+iv分别对应实数对 (x,y)和 (u,v), 对于函数w=f(z),u、v为x、y 的二元实数函u(x,y)和 v(x,y),所以w=f(z)又常写成w=u(x,y)+iv(x,y)。 函数w=z 2+1.令z=x+iy,w=u+iv,那么 w=u+iv=(x+iy) 2+1=x 2 -y 2+1+2xyi, w=z 2+1对应于两个实函数 u=x 2 -y 2+1和v=2xy. 对于复变函数w=f(z)即u+iv=f(x+iy),可以理解为 两个复平面上的点集之间的映射,具体地说,复变 函数w=f(z)给出了z平面上的点集E到w平面上的点集 f(E)(或G)之间的一个对应关系: 其中w称为z的像, z称为w的原像. → z E w f z G ( )

例2.1函数w=二将z平面上的直线=1变成w平面上 的何种曲线? 1= x-iy 解:z=x+iy,w=u+iv=-= x+iy x2+y2 X y u= x2+y’ x2+y2 平面上的直线x=1对应于w平面上的曲线 y u- +y2 1+y2 2+v2= 1+yy++y 之平面 w平面 =1l 1+y x=1 4
例2.1 函数 将z平面上的直线 x=1变成w 平面上 的何种曲线? 1 w z = 解: 2 2 1 1 i i , i i x y z x y w u v z x y x y − = + = + = = = + + 2 2 2 2 , x y u v x y x y = = − + + z平面上的直线x=1对应于w平面上的曲线 2 2 1 , 1 1 y u v y y = = − + + 2 2 2 2 2 2 2 2 1 (1 ) (1 ) 1 1 y u v y y u y + = + + + = = + 1 1 2 2 ( ) 2 4 u v − + =

设函数w=z)定义在E上,值域为G.若对于G中的 任一点w,在E中存在一个或几个点z与之对应,则在G 上确定了一个单值或多值函数,记作=f1(w),称为函 数w=孔z)的反函数 2.复变函数的极限 定义2.2设函数w=孔z)定义在z的去心邻域0<-z<r内, 若存在常数A,对于任意给定<0的,都存在一正数δ (0<心r),使得当0<z-zoK时,有 f(z)-A<6, 则称函数z)当z→z时的极限存在,常数A为其极限值 记作 lim f(z)=4 2→20 或f(z)→A(z→0)
设函数w=f(z)定义在E上,值域为G.若对于G中的 任一点w,在E中存在一个或几个点z与之对应,则在G 上确定了一个单值或多值函数,记作z=f -1 (w),称为函 数w=f(z)的反函数. 2.复变函数的极限 定义2.2 设函数w=f(z)定义在z0的去心邻域0<|z-z0 |<r内, 若存在常数A,对于任意给定<0的,都存在一正数 (0<r),使得当0<|z-z0 |< r时,有 , 则称函数f(z)当z→z0时的极限存在,常数A为其极限值. 记作 或 . f z A ( ) − 0 lim ( ) z z f z A → = 0 f z A z z ( ) ( ) → →