
概率论与数理统计 A B B ACB AUB A∩B A B A-B B 2 2 A A∩B=☑ A B 上二页 下一页返回
A B B A A B B A A B B A A B A B A B A− B AB = A A 上一页 下一页 返 回
概率论与数理统计 事件的运算律 (1)交换律:AUB=AUB,AB=BA (2)结合律(AUB)UC=AU(BUC) (A∩B)∩C=A∩(B∩C) (3)分配律:A∩(BUC)=(A∩B)U(A∩C) AU(B∩C)=(AUB)∩(AUC) (4)德·摩根律(De Morgan): U4,=∩4,∩4,=UA, i=1 i=l i=1 i=1 U4,=∩4,∩4=UA. i=1 i=l i= 1 上一园下一页返回
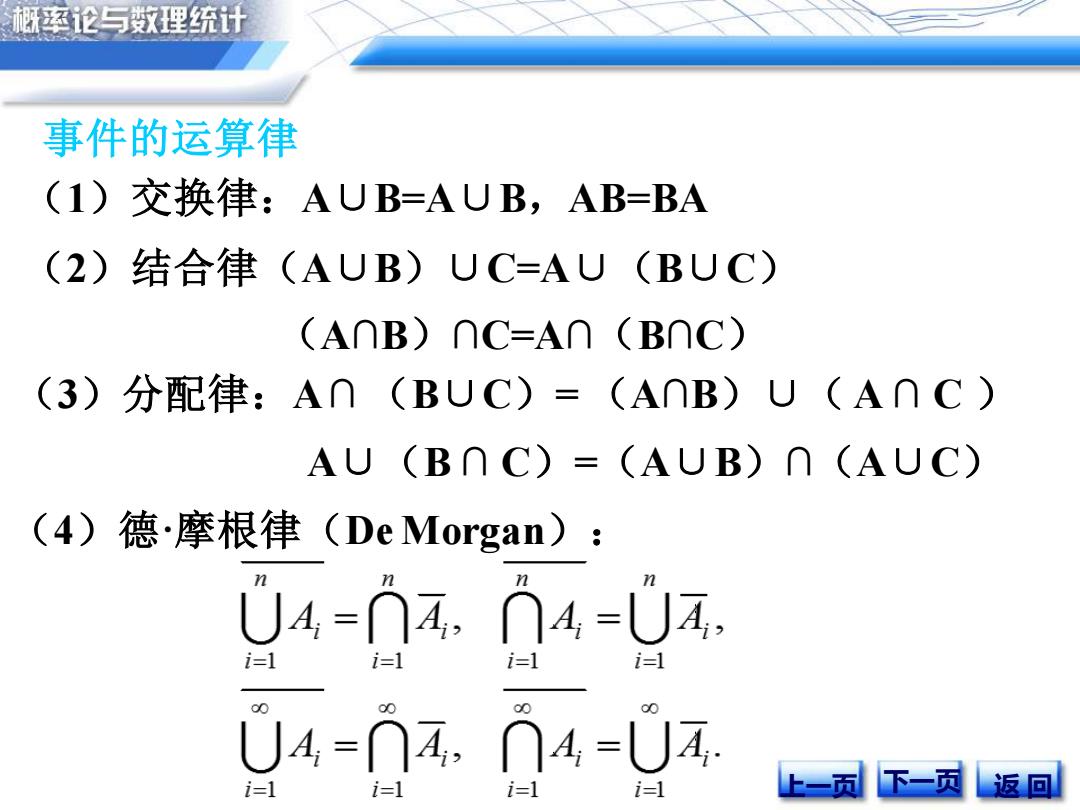
事件的运算律 (1)交换律:A∪B=A∪B,AB=BA (2)结合律(A∪B)∪C=A∪(B∪C) (3)分配律:A ∩ (B∪C)= (A∩B)∪( A ∩ C ) (A∩B)∩C=A∩(B∩C) A∪(B ∩ C)=(A∪B)∩(A∪C) (4)德·摩根律(De Morgan): 上一页 下一页 返 回

概率论与数理统计 例1.1设A,B,C为3个事件,用A,B,C的运算式表示下列事件: (1)A发生而B与C都不发生:ABC或A-B-C或A-(BUC) (2)A,B都发生而C不发生:ABC或AB-C (3)A,B,C至少有一个事件发生:AUBUC (4)A,B,C至少有两个事件发生:(AB)U(AC)U(BC) (5)A,B,C恰好有两个事件发生:(ABC)U(ACB)U(BCA) (6)A,B,C恰好有一个事件发生:(ABC)U(BAC)U(CAB) (7)A,B至少有一个发生而C不发生:(AUB)C (8)A,B,C都不发生:AUBUC或ABC 上一页 下一页返回
上一页 下一页 返 回 例1.1 设A,B,C为3个事件,用A,B,C的运算式表示下列事件: (1) A发生而B与C都不发生: (2) A,B都发生而C不发生: (3) A,B,C至少有一个事件发生: (4) A,B,C至少有两个事件发生: (5) A,B,C恰好有两个事件发生: (6) A,B,C恰好有一个事件发生: (7) A,B至少有一个发生而C不发生: (8) A,B,C ABC A B C A B C 或 − − − 或 ( ). ABC AB C 或 − . A B C. ( ) ( ) ( ). AB AC BC ( ) ( ) ( ). ABC ACB BC A ( ) ( ) ( ). ABC BAC C AB ( ) . A B C A B C ABC 或

概率论与数理统计 第二节 概率、古典概型 1、频率 定义1.1:在相同条件下,进行了n次试验.若随机事件A 在这n次试验中发生了k次,则比傅n称为事件A在n 次试验中发生的频率,记为.(①= n 频率具有下列性质: (1)对于任一事件A,有0≤fn(A)≤1 (2)fn(2)=1 上二页 下一页返回
第二节 概率、古典概型 1、频率 定义1.1: 在相同条件下,进行了n次试验.若随机事件A 在这n次试验中发生了k次,则比值 称为事件A在n 次试验中发生的频率,记为 频率具有下列性质: (1)对于任一事件A,有 (2) 上一页 下一页 返 回

概率论与数理统计 (3)若事件A,B互不相容,则 A(AUB)=(A)+(B) 一般,若A1,A2,…,Am互不相容,则 fnUA)=∑fn(A) i=1 i=1 上一园下一页返回
上一页 下一页 返 回