
00 因为实数项级数∑a和∑bm收敛的必要条件是 n=1 n= lim a,=0和limb=0. 必要条件 n→oo n->oo 所以复数项级数∑,收敛的必要条件是 lima,=0 1n>0o n=1 00 重要结论: lima≠0→级数∑n发散. n→oo n=] 启示:判别级数的敛散性时,可先考察iman0 1>00 lima≠0, 级数发散; 1→o0 如果{ liman =0, 应进一步判断. n-→o0
= =1 n 1 n n 因为实数项级数 an和 b 收敛的必要条件是 lim = 0 lim = 0 . → → n n n n a 和 b lim = 0 → n n 必 要 条 件 重要结论: lim 0 . 1 级数 发散 = → n n n n 所以复数项级数 收敛的必要条件是 n=1 n 启示: 判别级数的敛散性时, 可先考察 lim = 0 → n n ? → lim 0, n n 如果 级数发散; 应进一步判断. lim = 0, → n n

3.绝对收敛与条件收敛 定理三如果∑an收敛,那末∑an也收敛. n= n=] 且不等式2a≤∑a成立, m=1 =1 注意 ∑&n的各项都是非负的实数, n=1 应用正项级数的审敛法则判定
3. 绝对收敛与条件收敛 , . 1 1 如 果 收 敛 那 末 也收敛 = = n n n n . 1 1 且不等式 成 立 = = n n n n 注意 , 1 的各项都是非负的实数 n= n 应用正项级数的审敛法则判定. 定理三

证 由于∑a=∑a,2+b, 而n≤Vn2+bn,,b≤an+b., 根据实数项级数的比较准测,知 ∑4n及∑bn都收敛, n=1 n=1 故∑an及∑b也都收敛。 n-l n=l
证 由于 , 1 2 2 1 = = = + n n n n n a b 而 , , 2 2 2 2 an an + bn bn an + bn 根据实数项级数的比较准则, 知 , 1 1 及 都收敛 = = n n n an b . 1 1 故 及 也都收敛 = = n n n an b
0 由定理二可得∑an是收敛的. n=1 又由 asab k=1 k=1 可知 lim .u k= 或 2 [证毕] k-1 =1
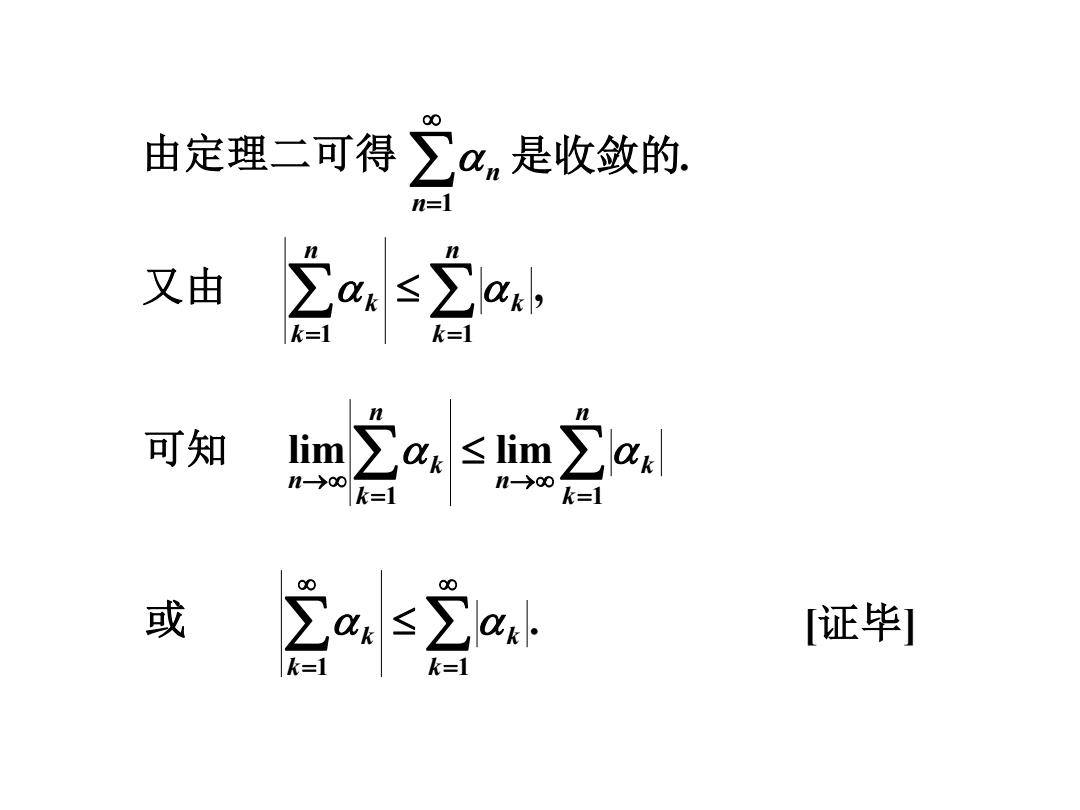
由定理二可得 . 1 是收敛的 n= n , 1 1 = = n k k n k 又由 k = → = → n k k n n k k n 1 1 可知 lim lim . [证毕] 1 1 = = k k k 或 k

定义 如果∑an收敛,那末称级数∑an为绝对收敛. n=1 n=1 非绝对收敛的收敛级数称为条件收敛级数. 由于 a≤V☑+ b≤/听+ 00 00 00 ∑an绝对收敛台∑an与∑bn绝对收敛 n= n=1 n=]
非绝对收敛的收敛级数称为条件收敛级数. 由于 ≤ 2 2 an an bn + 如果 收敛, 那末称级数 为绝对收敛. n=1 n n=1 n 定义 ≤ 2 2 bn an bn + . 1 1 1 绝对收敛 与 绝对收敛 = = = n n n n n n a b