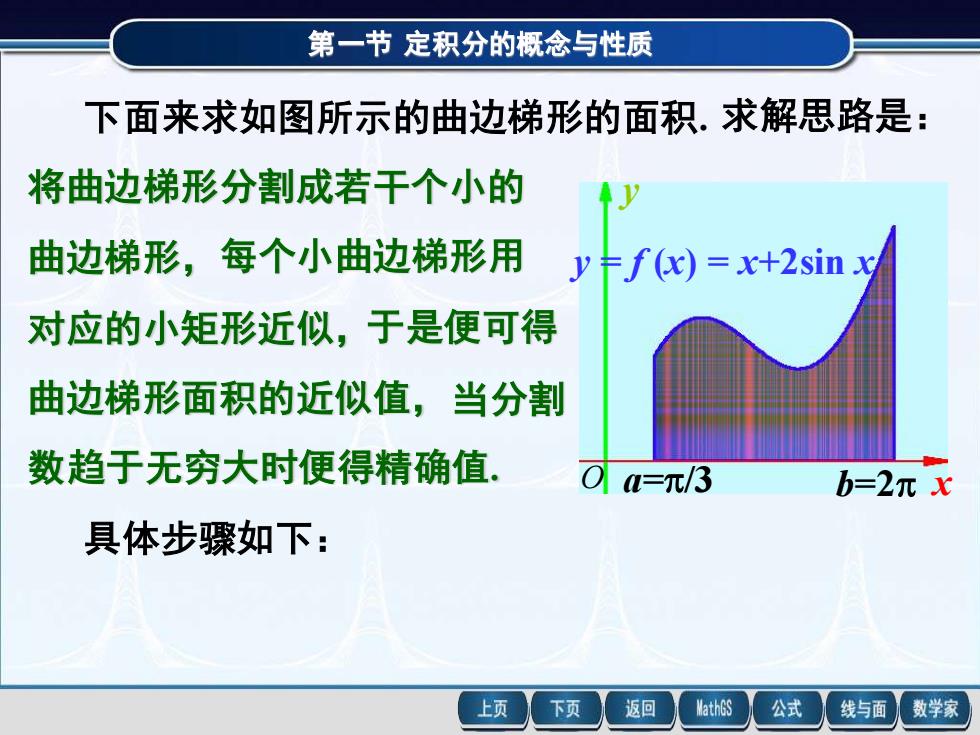
第一节定积分的概念与性质 下面来求如图所示的曲边梯形的面积.求解思路是: 将曲边梯形分割成若干个小的 曲边梯形,每个小曲边梯形用 y=f(x)=x+2sinx 对应的小矩形近似,于是便可得 曲边梯形面积的近似值,当分割 数趋于无穷大时便得精确值. M=元/3 b=2元x 具体步骤如下: 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 下面来求如图所示的曲边梯形的面积. 求解思路是: 将曲边梯形分割成若干个小的 曲边梯形,每个小曲边梯形用 对应的小矩形近似,于是便可得 曲边梯形面积的近似值,当分割 数趋于无穷大时便得精确值. 具体步骤如下: a=/3 b=2 x y y = f (x) = x+2sin x O
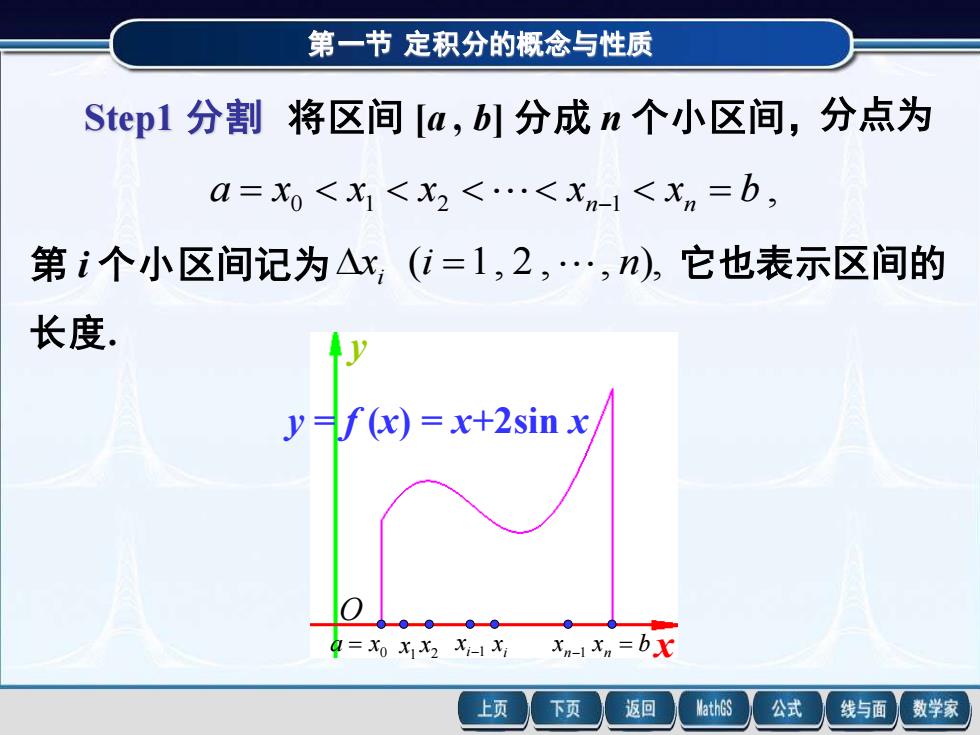
第一节定积分的概念与性质 Step1分割将区间[a,b]分成n个小区间,分点为 a=x0<x<X2<.<X-<X=b, 第i个小区间记为△x(i=1,2,.,n),它也表示区间的 长度, y=f(x)=x+2sin x a=X0 XX2 Xi-X Xn-1X=bx 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 Step1 分割 将区间 [a , b] 分成 n 个小区间,分点为 , a = x0 x1 x2 xn−1 xn = b 第 i 个小区间记为 x (i 1, 2 , , n), i = 它也表示区间的 长度. x y y = f (x) = x+2sin x 0 a = x 1 x 2 x i−1 x i x n−1 x x b n = O

第一节定积分的概念与性质 Step2近似以每个小区间为底,以f(5)(5,∈△x) 为高作矩形,并以矩形来近似相应的小曲边梯形 y=f(x)=x+2sin x y=f(x)=x+2sin x Q=xx为2xx,xm-1xn=bX 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 Step2 近似 以每个小区间为底,以 ( ) ( ) i i i f x 为高作矩形,并以矩形来近似相应的小曲边梯形. x y y = f (x) = x+2sin x 0 a = x 1 x 2 x i−1 x i x n−1 x x b n = O x y y = f (x) = x+2sin x O
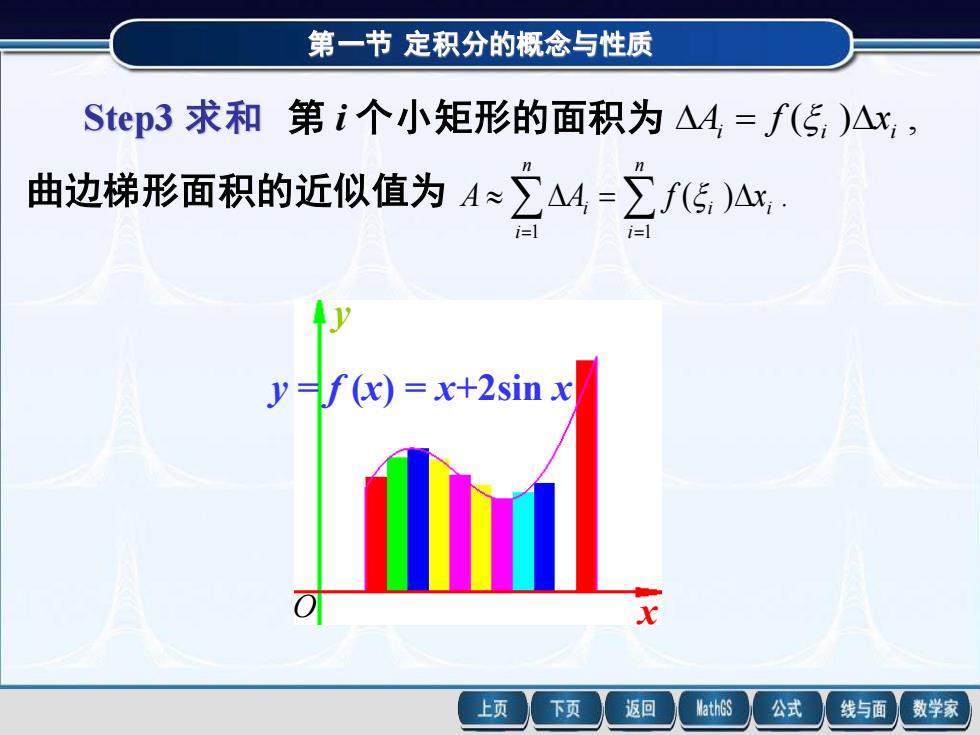
第一节定积分的概念与性质 Step3求和第i个小矩形的面积为△A=f(5,)△x, 曲边梯形面积的近似值为A≈∑AA=∑f(传,)Ax y=f(x)=x+2sin x 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 Step3 求和 第 i 个小矩形的面积为 ( ) , i i i A = f x 曲边梯形面积的近似值为 ( ) . 1 1 = = = n i i i n i i A A f x x y y = f (x) = x+2sin x O

第一节定积分的概念与性质 Step4取极限 A=lim2A4=lim2f传)ax, 10 0 i=l 其中2为n个小区间长度中的最大值. y=f(x)=x+2sin x yf(x)=x+2sin x 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 Step4 取极限 其中 为 n 个小区间长度中的最大值. ( ) , 0 1 0 1 lim lim → = → = = = n i i i n i i A A f x x y y = f (x) = x+2sin x O x y y = f (x) = x+2sin x O