《高等数学》课程教学资源（课件讲稿）第九章 多元函数微分学_0906多元函数微分学的几何应用

63、一元向量值函数的导数定义 2 设向量值函数r=f(t)在点t,的某一邻域内有定义． 如果Ar于(t+AI)-T()存在，则称这个极限向量为向量值函数limlimAtN->0 NtN-0了-T(0)在点,处的导数或导向量 记作子(1)或“dt r=t设向量值函数π=f(t),tED，若D, C D，f(t)在D,中的每一点都存在导向量子(1) (或),则称子(1)在D,上可导.dt向量值函数F(t)=(f,(t),f,(t),fs(t))在点t,可导的充分必要条件是它的三个分量函数fi(t),f,(t),f,(t)在点t,均可导此时有 F'(t)=（ f<(t.), f’(t.), f'(t))001018个不不高教学教学部不不不

高等数学教学部 6

设ü(t)、(t)是可导的向量值函数，℃为常向量，c为任一常数，β(t)是可导的数量函数，则(2) (cn) = cn;c=0;(1)dtdtd(4) *(ou) = pu + pn';(3)(u±)=ü±;一dtdt(S)(un) =u'+us';6)"(ux)=u'x+ux;dtdtd(7)u[p(t)l=u'lp(t)lp'(t)dt008个不不高尊数学教学部不不不

高等数学教学部 7 (1) C  0; dt d  (2) (cu) cu ; dt d     (3) (u v ) u v ; dt d          (4) ( u) u u ; dt d           (5) (uv ) u v uv ; dt d           (6) (u v ) u v u v ; dt d             (7) u[ (t)] u [ (t)] (t). dt d       

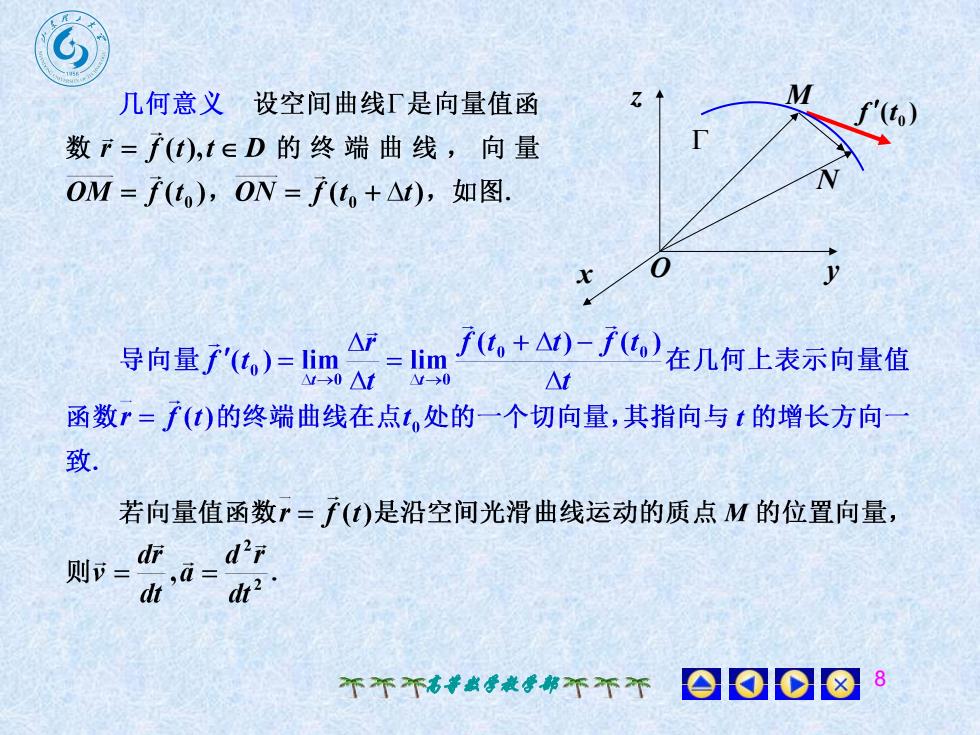
MZ几何意义设空间曲线是向量值函f'(t)数r=(t),tED的终端曲线， 向量NOM = f(t), ON = f(t. +△t), 如图0yx了(t,+ )-(t)在几何上表示向量值Ar导向量于'(t,）=limlimNtN->0M->0At函数r = f(t)的终端曲线在点t,处的一个切向量，其指向与t的增长方向一致.若向量值函数r=f(t)是沿空间光滑曲线运动的质点M的位置向量，drd'r则=,a=dt?dt8008个个个高等数学教学部

高等数学教学部 8 x y z M N O ( ) 0 f  t 

例 1 设空间曲线I的向量方程为r = f(t)=(t2 +1,4t-3,2t2-6t),求曲线厂在t=2处的单位切向量解 : '(t) =(2t,4,4t -6), F'(2)=(4,4,2),所求单位切向量为 ±=(4,4,2), 即 ±=(2,2,1)36例2一个人在悬挂式滑翔机上由于快速上升气流而沿位置向量r=f(t)=3cost.i+3sint.j+t2k的路径螺旋式向上，求（1）滑翔机的速度向量和加速度向量；(2）滑翔机的速率;（3）滑翔机的加速度与速度正交的时刻解 (l) r=F(t)=3cost.i+3sint.j+t'k,.:. v = f'(t)=-3sint.i +3cost.j + 2tk,a = f"(t)=-3cost.i -3sint.j+2k.(2)=~9+4t(3) i.a= 4t = 0= t = 0.0008中个不高教学教学部不不不

高等数学教学部 9 f (t)  (2t,4,4t  6),   f (2)  (4,4,2),  (4,4,2), 6 1  (2,2,1). 3 1  (1) ( ) 3cos 3sin , 2 r f t t i t j t k            v f (t) 3sint i 3cost j 2tk,               a f (t) 3cost i 3sint j 2k.              (2) 9 4 . 2 v   t  (3) v  a  4t  0  t  0.  