
行列试 §1.2行列式的性质 行列式的性质 二、 应用举例 三、小结思考题
第一章 行列式 三、小结 思考题 二、应用举例 一、行列式的性质 §1.2 行列式的性质

第一章行列式 、 行列式的性质 利用行列式的定义计算行列式,特别是高阶 行列式,计算量相当大.为简化行列式的计算,下 面我们来讨论行列式的性质. 由行列式的定义式知,行列式可表示为第一行 的元素与其对应的代数余子式的乘积之和,即行列 式可按第一行的展开式,事实上,行列式可按任意 一行(列)展开. 有下面的重要定理
第一章 行列式 一 、行列式的性质 利用行列式的定义计算行列式,特别是高阶 行列式,计算量相当大.为简化行列式的计算,下 面我们来讨论行列式的性质. 由行列式的定义式知,行列式可表示为第一行 的元素与其对应的代数余子式的乘积之和,即行列 式可按第一行的展开式,事实上,行列式可按任意 一行(列)展开. 有下面的重要定理

第一章行列式 定理1.2.1n阶行列式等于它的任意一行(列)的元素 与其对应的代数余子式的乘积之和,即 D=41A+a2A2+.+0nAn(i=1,2,.,n) 或 D=1A+a2jA2j+.+0时A( j=1,2,.,n) 推论如果n阶行列式中的行所有元素除4:外都为 零,那么行列式就等于:与其对应的代数余子式 的乘积,即 D=anAj
第一章 行列式 定理1.2.1 n阶行列式等于它的任意一行(列)的元素 与其对应的代数余子式的乘积之和,即 1 1 2 2 . ( 1,2, , ) D i i i i in in a A a A a A i n 1 1 2 2 . ( 1, 2, , ) D j j j j nj nj a A a A a A j n 或 ij a ij 零,那么行列式就等于 a 推论 如果n阶行列式中的i行所有元素除 外都为 与其对应的代数余子式 的乘积,即 D ij ij a A
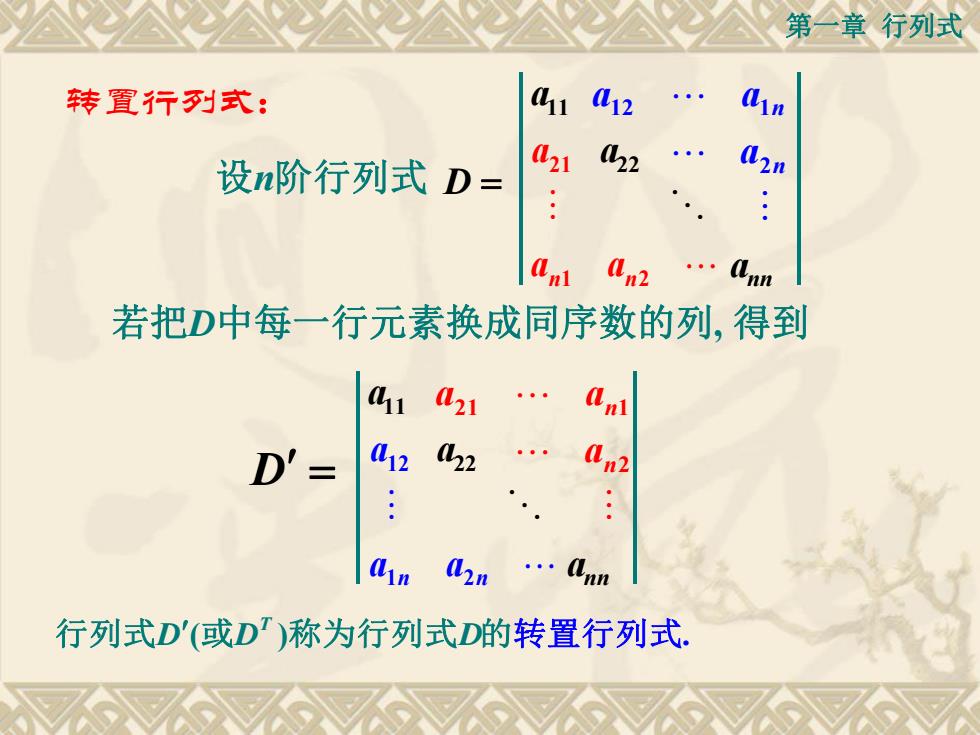
第一章行列式 转置行列式: 1 12 设n阶行列式D= 21 L22 0n2 .ln 若把D中每一行元素换成同序数的列,得到 1 021 D'= 12 2 02 .: .lnn 行列式D'(或D')称为行列式D的转置行列式
第一章 行列式 设n阶行列式 nn a a a 22 11 n n a a a 2 12 1 1 2 21 n n a a a D 2 21 1 n n a a a n n a a a 1 2 D 12 nn a a a 22 11 若把D中每一行元素换成同序数的列, 得到 ( ) . T 行列式D 或D 称为行列式D的转置行列式 转置行列式:

第一章行列式 性质1行列式与它的转置行列式相等. 例当=2时,11012 011421 结论成立 021022 012L22 说明 行列式中行与列具有同等的地位,因此行列 式的性质凡是对行成立的对列也同样成立
第一章 行列式 11 12 11 21 21 22 12 22 a a a a a a a a 例 当n=2时, ,结论成立. 说明 行列式中行与列具有同等的地位,因此行列 式的性质凡是对行成立的对列也同样成立