《线性代数》课程电子教案（C）第四章线性方程组 4-2 齐次线性方程组

§4.2齐次线性方程组 设齐次线性方程组 a31+ax2+.+=0 az+azx+.+a=0 (4-5) a+amx2+.+a=0 其系数矩阵 a41a12.ain 令 x x= 0 则线性方程组(4-5)的矩阵方程形式为 Ax=0. (4-6) 显然，线性方程组(45)总是有解的. 若x,x2,.,xn为(45)的解，则 x= 是(4-6)的解，也是线性方程组(4-5)的解向量. 线性方程组(4-5)的解向量具有下面两个重要性质. 性质1齐次线性方程组的两个解向量的和仍然是解向量，即设5,5，是(45)的解向 量，则5+5，也是(45)的解向量 证只需验证气+52满足线性方程组(4-6)即可.因为5,5，是(4-5)的解向量，所以 A5,=0,A52=0,而A51+52)=A5,+A52=0+0=0.故5+5满足(4-6)，即为(4-5)

§4.2 齐次线性方程组 设齐次线性方程组                0 0 0 1 1 2 2 21 1 22 2 2 11 1 12 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x (4-5) 其系数矩阵               m m mn n n a a a a a a a a a A 1 2 21 22 2 11 12 1 . 令        n x x x x 2 1 ，        0 0 0 0 . 则线性方程组(4-5)的矩阵方程形式为 Ax  0 . (4-6) 显然，线性方程组(4-5)总是有解的. 若 n x , x , , x 1 2  为(4-5)的解，则        n x x x x 2 1 是(4-6)的解，也是线性方程组(4-5)的解向量. 线性方程组(4-5)的解向量具有下面两个重要性质. 性质 1 齐次线性方程组的两个解向量的和仍然是解向量，即设 1 2  , 是(4-5)的解向 量，则 1   2也是 (4-5)的解向量. 证 只需验证 1  2 满足线性方程组(4-6)即可.因为 1 2  , 是(4-5)的解向量，所以 0 A 1  ， 0 A 2  ，而 ( ) 0 0 0 A  1   2  A 1  A 2    .故 1  2满足(4-6)，即为(4-5)

的解向量 性质2齐次线性方程组的一个解向量的倍数仍为解向量，即设5是(45)的解向量， 1是任意数，则5也是(45)的解向量. 证由于A(15)=2(A)=0=0,所以5是(4-5)的解向量. 由性质1与性质2知，齐次线性方程组(45)的解向量的线性组合仍是(45)的解向 量，即设52,52,5都是(45)的解向量，1,2.元n为任意数，则 25+元252+.+n-5n 仍是(45)的解.因此，方程组(45)的全部解向量构成一个向量空问，称之为方程组(45) 的解空间，它是R的一个子空间. 如果方程组(4-5)有非零解，由性质1与性质2知，它一定有无穷多非零解.要求出 (45)的所有解，只需求出解空间的一组基就行了. 下面我们来给出求解空间的一组基的一种方法 设线性方程组(4-5)系数矩阵A的秩r(<),不妨假设A的前r个列向量线性无关，于 是A的行最简形为 [1.0bH.bn 01bn.bn 0.00.0 。 . 0.00.0」 【对应的线性方程组为 =-b.-baXn (4-7) x =-brx-brax 显然，线性方程组(4-5)与(47)同解.在(47)中，任给x41,x。一组值，可唯一确定 x,x2,x,的值，就得到(4-7)的一个解，也就是(4-5)的解.我们把x1,xn称为自由 未知量 令x1,xn分别取下列n-r组数：

的解向量. 性质 2 齐次线性方程组的一个解向量的倍数仍为解向量，即设 是(4-5)的解向量，  是任意数，则 也是(4-5)的解向量. 证 由于 A( )  (A )  0  0，所以 是(4-5)的解向量. 由性质 1 与性质 2 知，齐次线性方程组(4-5)的解向量的线性组合仍是(4-5)的解向 量，即设    nr , , , 2 2 都是(4-5)的解向量，  nr , , 1 2 为任意数，则 1 1  2 2  nr nr 仍是(4-5)的解.因此，方程组(4-5)的全部解向量构成一个向量空间，称之为方程组(4-5) 的解空间，它是 n R 的一个子空间. 如果方程组(4-5)有非零解，由性质 1 与性质 2 知，它一定有无穷多非零解.要求出 (4-5)的所有解，只需求出解空间的一组基就行了. 下面我们来给出求解空间的一组基的一种方法. 设线性方程组(4-5)系数矩阵 A的秩r( n) ,不妨假设 A的前r 个列向量线性无关，于 是 A的行最简形为                            0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 1 rr rn r n b b b b I . I 对应的线性方程组为                   r r r r r n n r r n n x b x b x x b x b x , 1 1 , 1 1, 1 1 1, （4-7） 显然，线性方程组(4-5)与(4-7)同解.在(4-7)中，任给 r n x , , x 1  一组值，可唯一确定 r x , x , x 1 2  的值，就得到(4-7)的一个解，也就是（4-5）的解.我们把 r n x , , x 1  称为自由 未知量. 令 r n x , , x 1  分别取下列n  r 组数：

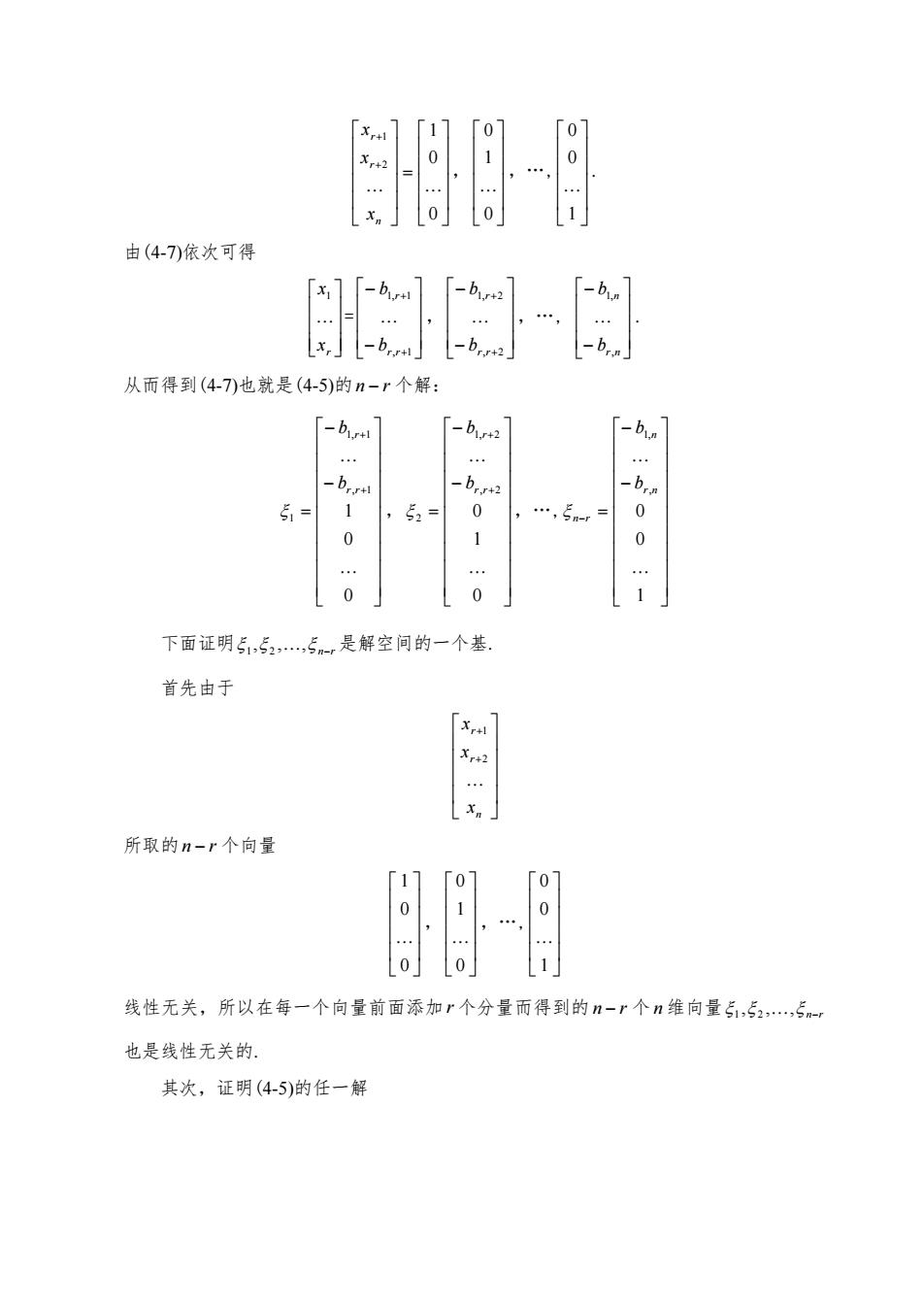
0 由(47)依次可得 从而得到(47)也就是(4-5)的n-r个解： [-b*2 「-bl b. -b,r42 51= 1 0 ，.,5 0 0 1 0 0 0 下面证明5,52.，5，是解空间的一个基. 首先由于 x42 x 所取的n-r个向量 1) 0 0 0 0 1 线性无关，所以在每一个向量前面添加r个分量而得到的n-r个n维向量5,52，5 也是线性无关的. 其次，证明(4-5)的任一解

                0 0 1 2 1 n r rx x x ，       0 1 0 ，.,       1 0 0 . 由(4-7)依次可得       r x x1 =           , 1 1, 1 r r r b b ，           , 2 1, 2 r r r b b ，.,        r n n b b , 1, . 从而得到(4-7)也就是(4-5)的n  r 个解：              0 0 1 , 1 1, 1 1 r r r b b  ，              0 1 0 , 2 1, 2 2 r r r b b  ，.,            1 0 0 , 1,r n n n r b b  下面证明    nr , , , 1 2 是解空间的一个基. 首先由于          n r rx x x 2 1 所取的n  r 个向量       0 0 1 ，       0 1 0 ，.,       1 0 0 线性无关，所以在每一个向量前面添加r 个分量而得到的 n  r 个 n 维向量    nr , , , 1 2 也是线性无关的. 其次，证明(4-5)的任一解

都可以由51,52.，5，线性表示.为此，构造向量 n=元r5+元r252++元5a-, 由于5,52，5是(45)的解，故n也是(4-5)的解.比较n与5知，它们的后面n-r个分 量对应相等，而线性方程组(4-刀表明它的任一解的前r个分量可由后-r个分量唯一确 定，因此刀=5，即 5=入15+252++元n5m- 这样就证明了5,52，5，是解空间的一个基，从而知解空间的维数是n-r 上面给出了一种求解空间的基的方法.当然，求基的方法很多，而解空间的基也不 唯一，事实上方程组(45)的任意n-r个线性无关的解向量，都可以作为解空间的基. 方程组(45)解空间的基又称为方程组的基础解系. 当方程组(4-5)的系数矩阵的秩()=n时，方程组(45)只有零解，因而没有基础解 系（此时解空问只有一个零向量）：当R(A)=r<n时，方程组(45)的基础解系必有含 n-r个向量. 设求得5,52,5。，为方程组(4-5)的一个基础解系，则(4-5)的任一解x可表示为 x=k5+k52+.+k-5n 其中k,k2,kn,为任意常数.上式称为方程组(45)的通解，此时解空间可表示为 (x=k5+k52++k。n5,k,k2,kn,为任意常数】. 由此可见，方程组(45)有非零解的充分必要条件为(A)=r<n,并且其基础解系 所含解向量的个数为n-r

        n r r      1 1 都可以由    nr , , , 1 2 线性表示.为此，构造向量   r1 1  r2 2  n nr ， 由于    nr , , , 1 2 是(4-5)的解，故 也是(4-5)的解.比较 与 知，它们的后面n  r 个分 量对应相等，而线性方程组(4-7)表明它的任一解的前r 个分量可由后n  r 个分量唯一确 定，因此   ，即   r1 1  r2 2  n nr 这样就证明了    nr , , , 1 2 是解空间的一个基，从而知解空间的维数是n  r . 上面给出了一种求解空间的基的方法.当然，求基的方法很多，而解空间的基也不 唯一，事实上方程组(4-5)的任意n  r 个线性无关的解向量，都可以作为解空间的基. 方程组(4-5)解空间的基又称为方程组的基础解系. 当方程组(4-5)的系数矩阵的秩 R(A)  n时，方程组(4-5)只有零解，因而没有基础解 系（此时解空间只有一个零向量）；当 R(A)  r  n 时，方程组(4-5)的基础解系必有含 n  r 个向量. 设求得    nr , , , 1 2 为方程组(4-5)的一个基础解系，则(4-5)的任一解 x 可表示为 n r n r x k k k  1 1  2 2     . 其中 n r k k k   , , , 1 2 为任意常数.上式称为方程组(4-5)的通解，此时解空间可表示为 { n r n r x k k k  1 1  2 2     | n r k k k   , , , 1 2 为任意常数}. 由此可见，方程组(4-5)有非零解的充分必要条件为 R(A)  r  n ，并且其基础解系 所含解向量的个数为n  r

例1解方程组 [x+2x2+2x3+x4=0, 2x1+x2-2x3-2x4=0, x1-x2-4x3-3x4=0 解对系数矩阵A进行初等行变换化为行最简形 「1221152-2r「12211 A=21-2-20-3-6-4 1-1-4-35-片0-3-6-4 10-2-引 5-4-2012 012 4 -3000 1 0003 因此，R(4)=2与原方程组同解的方程组为 -2-5x=0 +x+x,=0 即 x=2x+3 =-2xy-3 以xx作为自由未知量，令 [母 分别代如上面方程组，得到两个解 21 1 ,50 3 这两个解就组成原方程组的一个基础解系.因而方程组的通解为

例 1 解方程组                  4 3 0. 2 2 2 0, 2 2 0, 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x 解 对系数矩阵 A进行初等行变换化为行最简形                           0 3 6 4 0 3 6 4 1 2 2 1 ~ 2 1 1 4 3 2 1 2 2 1 2 2 1 3 1 2 1 r r r r A ) 3 1 (~ 2 3 2    r r r                0 0 0 0 3 4 0 1 2 3 5 1 0 2 ~ 2 0 0 0 0 3 4 0 1 2 1 2 2 1 1 2 r r . 因此， R(A)  2与原方程组同解的方程组为            0. 3 4 0, 3 5 2 2 3 4 1 3 4 x x x x x x 即           . 3 4 2 , 3 5 2 2 3 4 1 3 4 x x x x x x 以 3 4 x , x 作为自由未知量，令       4 3 x x =       0 1 ，       1 0 ， 分别代如上面方程组，得到两个解.        0 1 2 2  1 ，        3 0 4 5  2 . 这两个解就组成原方程组的一个基础解系.因而方程组的通解为