
全程设计 1.数列
1.数列

梳理·构建体系 归纳核心突破
梳理·构建体系 归纳·核心突破
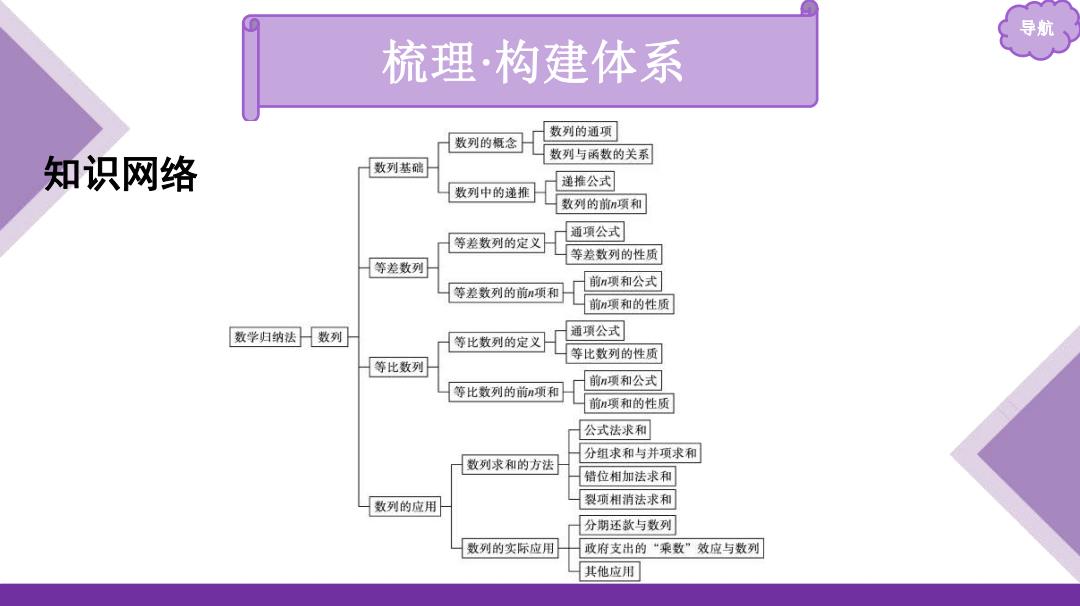
导航 梳理·构建体系 数列的通项 数列的概念 数列与函数的关系 知识网络 数列基础 递推公式 数列中的递推 数列的前n项和 等差数列的定义 通项公式 等差数列的性质 等差数列 前n项和公式 等差数列的前项和 前n项和的性质 数学归纳法 数列 等比数列的定义 通项公式 等比数列的性质 等比数列 前n项和公式 等比数列的前项和 前n项和的性质 公式法求和 分组求和与并项求和 数列求和的方法 错位相加法求和 数列的应用 裂项相消法求和 分期还款与数列 数列的实际应用 政府支出的“乘数”效应与数列 其他应用
导航 梳理 ·构建体系 知识网络

导 要点梳理 1.什么是数列?数列的分类有哪些?什么是数列通项公式和数 列递推公式?什么是数列的前项和?数列与函数之间具有怎 样的关系?请完成下表 概念 含义 数列、数按照 排列的一列数称为数列数列中的 列的项 都称为这个数列的项 项数 的数列称为有穷数列,项数 的数列 数列的分 称为无穷数列 类 递增数列:at1an;递减数列:ar+ l ani 常数列:an=nm,其中n∈N
导航 要点梳理 1.什么是数列?数列的分类有哪些?什么是数列通项公式和数 列递推公式?什么是数列的前n项和?数列与函数之间具有怎 样的关系?请完成下表. 概念 含义 数列、数 列的项 按照 一定次序排列的一列数称为数列.数列中的 每一个数 都称为这个数列的项 数列的分 类 项数 有限 的数列称为有穷数列,项数无限 的数列 称为无穷数列 递增数列:an+1 > an ;递减数列:an+1 < an ; 常数列:an+1=an ,其中n∈N+

导航 概念 含义 般地,如果数列的第n项a,与n之间的关系可以用 数列通项 来表示,其中fun)是关于n的不含其他未知数 公式 的表达式,则称上述关系式为这个数列的一个通项 公式 如果已知数列的首项(或前几项),且数列的相邻两项 数列递推 或两项以上的关系都可以用一个公式来表示,则称 (递归)公 这个公式为数列的递推关系(也称为递推公式或递 式 归公式)
导航 概念 含义 数列通项 公式 一般地,如果数列的第n项an与n之间的关系可以用 an=f(n) 来表示,其中f(n)是关于n的不含其他未知数 的表达式,则称上述关系式为这个数列的一个通项 公式 数列递推 (递归)公 式 如果已知数列的首项(或前几项),且数列的相邻两项 或两项以上的关系都可以用一个公式来表示,则称 这个公式为数列的递推关系(也称为递推公式或递 归公式)